【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )

转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
A. 当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得铅笔的概率大约是0.70
C. 如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得文具盒
参考答案:
【答案】D
【解析】分析:本题考查的是利用频率估计概率.
解析:从表格中可以看出:当n很大时,估计指针落在“铅笔”区域的频率大约是0.70,故A正确;用频率来估计概率,可以得出:假如你去转动转盘一次,获得铅笔的概率大约是0.70,故B正确;用频率来估计概率,可以得出:假如你去转动转盘一次,获得文具盒的概率大约是0.30,故如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次,故C正确;只是用频率来估算概率,并不是绝对的数据,所以转动转盘10次,不一定有3次获得文具盒,故D错误.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个样本有50个数据,其中最大值是208,最小值是169,最大值与最小值的差是______;如果取组距为5,那么这组数据应分成______组,第一组的起点为________,第二组与第一组的分点为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,m均为整数,且(x+a)(x+b)=x2+mx+36,则m可以取的值共有( )个?
A.0
B.5
C.10
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )

A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的对角线AC、BD交于O点,∠ABC的平分线交AC于E,交CD于F,∠DBF=15°,连结OF,则下列三角形①△AOD,②△COF,③△DOF,④△EOF中是等腰三角形的为________(填入序号)。
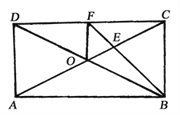
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个数为三位数,十位数字是a,个位数字比a小2,百位数字是a的2倍,则这个三位数可表示:( )
A. 21a-2 B. 211a-2 C. 200a-2 D. 3a-2
相关试题

