【题目】阅读下面材料并解决有关问题:
我们知道:|x|= .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式= .
.
通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
参考答案:
【答案】(1)原式 ;(2)
;(2)![]() 的最大值为2.
的最大值为2.
【解析】
(1)分为x<﹣2、﹣2≤x<4、x≥4三种情况化简即可;
(2)分x<﹣1、﹣1≤x≤1、x>1分别化简,结合x的取值范围确定代数式值的范围,从而求出代数式的最大值.
(1)令![]() 和
和![]() ,分别求得
,分别求得![]() ,x=4,(称-2,4分别为
,x=4,(称-2,4分别为![]() 和
和![]() 的零点值).
的零点值).
在实数范围内,零点值![]() 和
和![]() ,可将全体实数分成不重复且不遗漏的如下3种情况:
,可将全体实数分成不重复且不遗漏的如下3种情况:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
从而化简代数式![]() 可分以下3种情况:
可分以下3种情况:
(1)当![]() 时,原式
时,原式![]() ;
;
(2)当![]() 时,原式
时,原式![]() ;
;
(3)当![]() 时,原式
时,原式![]() .
.
综上所述:原式 .
.
(2)令x-1=0和x+1=0,分别求得x=1,x=-1.
在实数范围内,零点值x=-1和x=1,可将全体实数分成不重复且不遗漏的如下3种情况:
(1)x<-1;(2)![]() ;(3)
;(3)![]() .
.
从而化简代数式![]() 可分以下3种情况:
可分以下3种情况:
(1)当![]() 时,原式
时,原式![]() ;
;
(2)当![]() 时,原式
时,原式![]() ;
;
(3)当x>1时,原式![]() .
.
综上所述:![]() 的最大值为2.
的最大值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚.

(1)任意转动转盘一次,获得猴年邮票的概率是;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A、B、C分别表示有理数a、b、c.
(1)当n=1时,A、B、C三点在数轴上的位置如图所示,a、b、c三个数的乘积为正数.

①数轴上原点的位置可能( )
A.在点A左侧或在A、B两点之间
B.在点C右侧或在A、B两点之间
C.在点A左侧或在B、C两点之间
D.在点C右侧或在B、C两点之间
②若这三个数的和与其中的一个数相等,则a=_________(简述理由)
(2)将点C向右移动(n+2)个单位得到点D,点D表示有理数d,a、b、c、d四个数的积为正数,且这四个数的和与其中的两个数的和相等,a为整数,若n分别取1,2,3,…,100时,对应的a的值分别记为
 ,…,
,…, ,则
,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度
1:20
1:16
1:12
最大高度(米)
1.50
1.00
0.75

(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
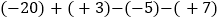 ;(2)
;(2)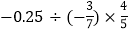 ;
;(3)
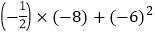 ; (4)
; (4)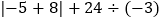 ;
;(5)
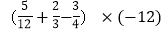 ; (6)
; (6)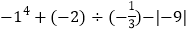 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.

(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,都是由边长为 1 的正方体叠成的立体图形,例如第⑴个图形由 1 个正方体叠成,第⑵个图形由 4 个正方体叠成,第⑶个图形由 10 个正方体叠成,依次规律,第⑺个图形由( )个正方形叠成.

A. 86 B. 87 C. 85 D. 84
相关试题

