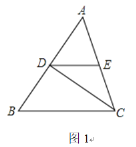
【题目】已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC,
(1)如果点E是边AC的中点,AC=5cm,求DE的长;
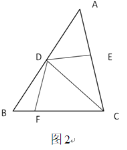
(2)如图2,若DE平分∠ADC,在BC边上取点F,使∠DFC=60°,若BC=7,BF=2,求DF的长.
参考答案:
【答案】(1)DE=2.5cm;(2)DF=3.
【解析】
(1)根据角平分线定义得到∠BCD =∠ACD,由于DE∥BC,根据平行线性质得∠EDC =∠BCD,则∠EDC =∠ACD,然后可得ED=EC,由点E是边AC的中点,AC=5cm得EC=2.5cm,所以DE=2.5cm;
(2)作DG⊥BC于点G,易求GB、GF的长,再根据在直角三角形中30°的锐角所对的直角边是斜边的一半即可求出DF的长.
解:(1)∵CD平分∠ACB,
∴∠BCD =∠ACD,
∵DE∥BC,
∴∠EDC =∠BCD,
∴∠EDC =∠ACD,
∴ED=EC,
∵点E是边AC的中点,AC=5cm,
∴EC=2.5cm,
∴DE=2.5cm;
(2)作DG⊥BC于点G,

∵DE∥BC,
∴∠ADE=∠B,∠EDC=∠DCB,
∵DE平分∠ADC,
∴∠ADE=∠EDC,
∴∠B=∠DCB,
∴DB=DC.
∵DG⊥BC,
∴GB=![]() BC=
BC=![]() ×7=3.5,
×7=3.5,
∴GF=GBBF=3.52=1.5,
∵Rt△DGF中,∠DFG=60°,
∴∠FDG=30°
∴DF=2GF=2×1.5=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的角满足下列条件:①
的角满足下列条件:①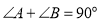 ;②
;②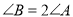 ,
,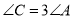 ;③
;③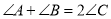 ;④
;④ ,
,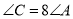 ,其中一定不是直角三角形的是______.(只填序号)
,其中一定不是直角三角形的是______.(只填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第20个“上”字需用多少枚棋子( )

A. 78 B. 82 C. 86 D. 90
-
科目: 来源: 题型:
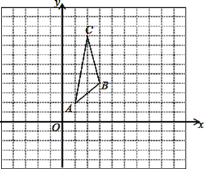
查看答案和解析>>【题目】在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)直接写出△ABC上点M(x,y)在上述变换过程中得到的对应点M2的坐标.
(3)直接写出△A1B1C1关于x轴对称后三个顶点A2、B2、C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:有两条边相等的三角形叫做等腰三角形。类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
(1)请你写出一个等对边四边形的名称;
(2)如图,在△ABC中,点D、E分别在AB、AC上,设CD、BE相交于点O,若∠A=50°,
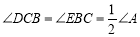 .请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);
.请写出图中其余等于50°的角,并猜想图中哪个四边形为等对边四边形(不需证明);(3)在
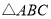 中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且
中,如果∠A是不等于50°的锐角,点D、E分别在AB、AC上,且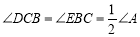 .探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.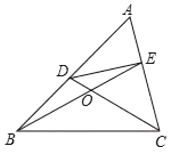
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为
 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖 -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A.
 B.
B. 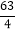 C. 16D. 14
C. 16D. 14
相关试题

