【题目】已知![]() 的角满足下列条件:①
的角满足下列条件:①![]() ;②
;②![]() ,
,![]() ;③
;③![]() ;④
;④![]() ,
,![]() ,其中一定不是直角三角形的是______.(只填序号)
,其中一定不是直角三角形的是______.(只填序号)
参考答案:
【答案】④
【解析】
依据三角形内角和定理进行计算,即可得到结论.
解:①当∠A+∠B=90°,根据三角形内角和可知,∠C=180°![]() 90°=90°,可以判定△ABC是直角三角形;
90°=90°,可以判定△ABC是直角三角形;
②当∠B=2∠A,∠C=3∠A,根据三角形内角和可知,∠A=30°,∠B=60°,∠C=90°,可以判定△ABC是直角三角形;
③当∠A+∠B=2∠C,根据三角形内角和可知,∠C=60°,∠A+∠B=120°,∠A和∠B中可能有一个角是90°,也可能没有,可以判定△ABC可能是直角三角形;
④当∠B=3∠A,∠C=8∠A,根据三角形内角和可知,∠A=15°,∠B=45°,∠C=120°,可以判定△ABC不可能是直角三角形;
综上所述:△ABC是直角三角形的有①②,可能是直角三角形的有③,一定不是直角三角形的是④;
故答案为④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
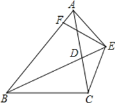
A.①②③B.①③④C.①②④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线交x轴于A、B两点,交y轴于C点,A点坐标为(﹣1,0),OC=2,OB=3,点D为抛物线的顶点.
(1)求抛物线的解析式;
(2)P为坐标平面内一点,以B、C、D、P为顶点的四边形是平行四边形,求P点坐标;
(3)若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S,求出定值S及M1、M2、M3这三个点的坐标.
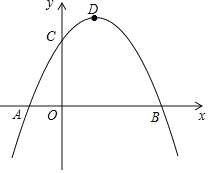
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
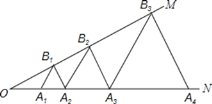
A. 64B. 32C. 16D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第20个“上”字需用多少枚棋子( )

A. 78 B. 82 C. 86 D. 90
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)直接写出△ABC上点M(x,y)在上述变换过程中得到的对应点M2的坐标.
(3)直接写出△A1B1C1关于x轴对称后三个顶点A2、B2、C2的坐标.
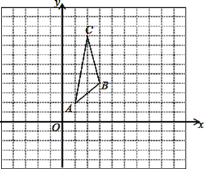
-
科目: 来源: 题型:
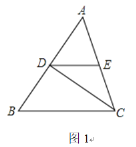
查看答案和解析>>【题目】已知△ABC中,∠ACB的平分线CD交AB于点D,DE∥BC,
(1)如果点E是边AC的中点,AC=5cm,求DE的长;
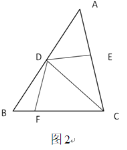
(2)如图2,若DE平分∠ADC,在BC边上取点F,使∠DFC=60°,若BC=7,BF=2,求DF的长.
相关试题

