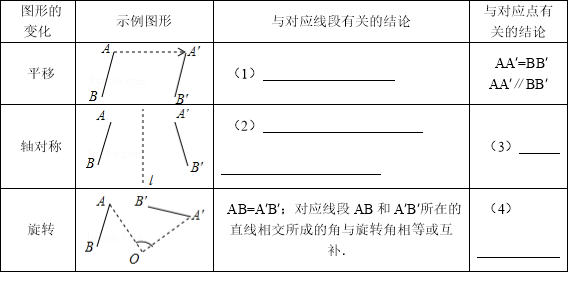
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
参考答案:
【答案】(1)AB=A′B′,AB∥A′B′;(2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上;(3)l垂直平分AA′;(4)OA=OA′,∠AOA′=∠BOB′.
【解析】
试题分析:(1)根据平移的性质即可得到结论;
(2)根据轴对称的性质即可得到结论;
(3)同(2);
(4)由旋转的性质即可得到结论.
试题解析:(1)平移的性质:平移前后的对应线段相等且平行.所以与对应线段有关的结论为:AB=A′B′,AB∥A′B′;
(2)轴对称的性质:AA′=BB′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上.
(3)轴对称的性质:轴对称图形对称轴是任何一对对应点所连线段的垂直平分线.所以与对应点有关的结论为:l垂直平分AA′.
(4)OA=OA′,∠AOA′=∠BOB′.
故答案为:(1)AB=A′B′,AB∥A′B′;(2)AB=A′B′;对应线段AB和A′B′所在的直线如果相交,交点在对称轴l上;(3)l垂直平分AA′;(4)OA=OA′,∠AOA′=∠BOB′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解分式方程.
(1)
(2)
-
科目: 来源: 题型:
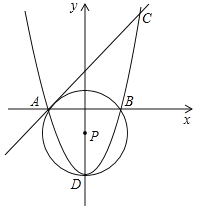
查看答案和解析>>【题目】(14分)在平面直角坐标系中,已知点A(﹣2,0),B(2,0),C(3,5).
(1)求过点A,C的直线解析式和过点A,B,C的抛物线的解析式;
(2)求过点A,B及抛物线的顶点D的⊙P的圆心P的坐标;
(3)在抛物线上是否存在点Q,使AQ与⊙P相切,若存在请求出Q点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底? -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把分子为1的分数叫做单位分数,如
 …,任何一个单位分数都可以拆分成两个不同的单位分数的和,如
…,任何一个单位分数都可以拆分成两个不同的单位分数的和,如  ,
,  ,
, 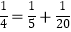 …观察上述式子的规律:
…观察上述式子的规律:
(1)把 写成两个单位分数之和;
写成两个单位分数之和;
(2)把 表示成两个单位分数之和.
表示成两个单位分数之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a<0,则关于x的不等式|a|x<a的解集是( )
A.x<1
B.x>1
C.x<﹣1
D.x>﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列顺序排列的等式:9
 0+1=1,9
0+1=1,9  1+2=11,9
1+2=11,9  2+3=21,9
2+3=21,9  3+4=31,9
3+4=31,9 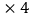 +5=41,……
+5=41,……
根据以上所反映的规律,猜想,第n个等式(n为正整数)应为( )
A.9(n-1)+n=10(n-1)+1
B.9n+n=(n-1)+n
C.9n+(n-1)=n2 -1
D.9n+n=10n+1
相关试题

