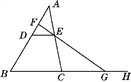
【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据三角形的外角性质得出∠EGH>∠B,再根据平行线的性质得出∠B=∠ADE,即可得出答案;(2)根据三角形的外角性质得出∠BFE=∠A+∠AEF,∠EGH=∠B+∠BFE,根据平行线的性质得出∠B=∠ADE,即可得出答案.
试题解析:
证明:(1)因为∠EGH是△FBG的外角,
所以∠EGH>∠B.
又因为DE∥BC,
所以∠B=∠ADE.
所以∠EGH>∠ADE.
(2)因为∠BFE是△AFE的外角,
所以∠BFE=∠A+∠AEF.
因为∠EGH是△BFG的外角,
所以∠EGH=∠B+∠BFE.
所以∠EGH=∠B+∠A+∠AEF.
又因为DE∥BC,所以∠B=∠ADE,
所以∠EGH=∠ADE+∠A+∠AEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(a﹣1)x2+3x﹣6的图象与x轴的交点为A和B,若点B一定在坐标原点和(1,0)之间,且B点不与原点和(1,0)重合,那么a的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为50°,则该三角形的底角为____.
-
科目: 来源: 题型:
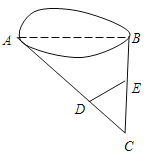
查看答案和解析>>【题目】如图,点D、E分别在AC、BC上,如果测得CD=20m,CE=40m,AD=100m,BE=20m,DE=45m,求A、B两地间的距离。
-
科目: 来源: 题型:
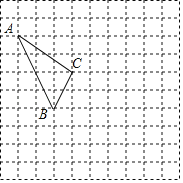
查看答案和解析>>【题目】在如图所示的正方形网络中,每个小正方形的边长为1,格点三角形(顶点是网络的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)点B关于x轴的对称点B2的坐标是 ;
(4)△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

-
科目: 来源: 题型:
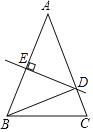
查看答案和解析>>【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长;
(2)若∠CBD=30°,试求△ABC三个角的度数.
相关试题

