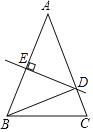
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长;
(2)若∠CBD=30°,试求△ABC三个角的度数.
参考答案:
【答案】(1)BE=6cm;(2)∠A=40°,∠ABC=70°,∠C=70°.
【解析】
(1)根据线段垂直平分线的性质得到AD=DB,AE=BE,根据三角形的周长公式求出AB,即可得出结论;
(2)根据等腰三角形的性质得到∠A=∠ABD=α,根据等腰三角形的性质、三角形内角和定理计算即可.
(1)∵DE是边AB的垂直平分线,
∴AD=DB,AE=BE.
∵△BCD的周长为18cm,
∴AC+BC=AD+DC+BC=DB+DC+BC=AC+BC=18(cm).
∵△ABC的周长为30cm,
∴AB=30﹣(AC+BC)=30﹣18=12(cm),
∴BE=12÷2=6(cm);
(2)设∠A=α.
∵DA=DB,
∴∠A=∠ABD=α.
∵AB=AC,
∴∠C=∠ABC=α+30°,
由三角形的内角和定理得:α+2(α+30°)=180°,
解得:α=40°,
∴∠A=40°,∠ABC=70°,∠C=70°.
-
科目: 来源: 题型:
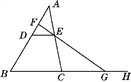
查看答案和解析>>【题目】如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证:
(1)∠EGH>∠ADE;
(2)∠EGH=∠ADE+∠A+∠AEF.
-
科目: 来源: 题型:
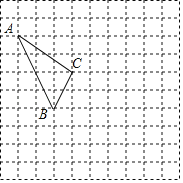
查看答案和解析>>【题目】在如图所示的正方形网络中,每个小正方形的边长为1,格点三角形(顶点是网络的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)点B关于x轴的对称点B2的坐标是 ;
(4)△ABC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

-
科目: 来源: 题型:
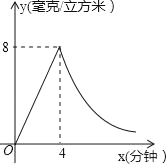
查看答案和解析>>【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,半径OC⊥AB交AB于点D,点P是⊙O上AB上方的一个动点(P不与A、B重合),已知∠APB=60°,∠OCB=2∠BCM.
(1)设∠A=α,当圆心O在∠APB内部时,写出α的取值范围;
(2)求证:CM是⊙O的切线;
(3)若OC=4,PB=4
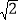 ,求PC的长.
,求PC的长.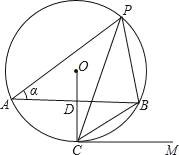
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

相关试题

