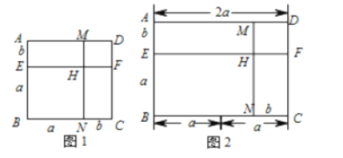
【题目】(1)我们已经知道,根据几何图形的面积关系可以说明完全平方公式,说明如下:如图1.正方形![]() 的面积=正方形
的面积=正方形![]() 的面积+(长方形
的面积+(长方形![]() +长方形
+长方形![]() 的面积)+正方形
的面积)+正方形![]() 的面积.即:
的面积.即:![]() .
.
(2)还有一些等式也可以用上述方式加以说明,请你尝试完成.如图2,长方形![]() 的面积=长方形
的面积=长方形![]() 的面积+长方形
的面积+长方形![]() 的面积-长方形
的面积-长方形![]() 的面积-________的面积,即
的面积-________的面积,即![]() ________________.
________________.
(3)计算![]() =______________.依照上述方法,画图并说明.
=______________.依照上述方法,画图并说明.
参考答案:
【答案】(2)正方形MHFD,2a2+ab﹣b2;(3)2a2+3ab+b2.
【解析】
(2)利用长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积计算.
(3)利用长方形ABCD的面积=正方形GBHF的面积+正方形FHQN的面积+长方形AGFE的面积+长方形EFNM的面积+长方形NQCO的面积+正方形MNOD的面积计算.
解:(2)长方形ABNM的面积=长方形EBCF的面积+长方形AEFD的面积﹣长方形HNCF的面积﹣正方形MHFD的面积,即:(2a﹣b)(a+b)=2a2+ab﹣b2.
故答案为:正方形MHFD,2a2+ab﹣b2.
(3)(2a+b)(a+b)=2a2+3ab+b2.
如图,

∵长方形ABCD的面积=正方形GBHF的面积+正方形FHQN的面积+长方形AGFE的面积+长方形EFNM的面积+长方形NQCO的面积+正方形MNOD的面积
∴(2a+b)(a+b)= a2+ a2+ ab+ ab+ ab+ b2=2a2+3ab+b2
故答案为:2a2+3ab+b2.
-
科目: 来源: 题型:
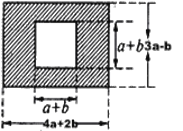
查看答案和解析>>【题目】眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a-b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
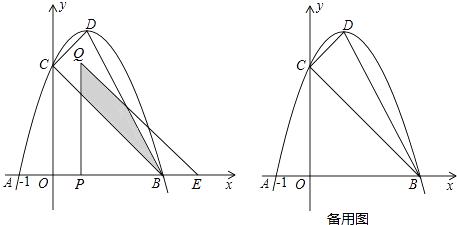
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )
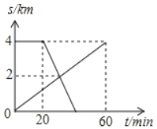
A. 8:30 B. 8:35 C. 8:40 D. 8:45
-
科目: 来源: 题型:
查看答案和解析>>【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-
 x+12(0<x<24)
x+12(0<x<24)C. y=2x-24(0<x<12) D. y=
 x-12(0<x<24)
x-12(0<x<24) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
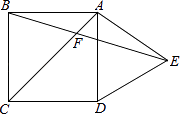
A.75°
B.60°
C.55°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=48°,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠An-1BC与∠An-1CD的平分线交于点An,要使∠An的度数为整数,则n的最大值为( )
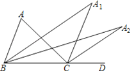
A.2B.3C.4D.5
相关试题

