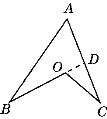
【题目】(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
x=____________°;x=____________°;x=____________°;
(3)如图③,一个六角星,其中∠BOD=70°,则∠A+∠B+∠C+∠D+∠E+∠F=________°.

参考答案:
【答案】(1)证明见解析. (2)180;180;180;(3)140
【解析】
(1)首先延长BO交AC于点D,可得BOC=∠BDC+∠C,然后根据∠BDC=∠A+∠B,判断出∠BOC=∠B+∠C+∠A即可.
(2)a、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.
b、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.
c、首先延长EA交CD于点F,EA和BC交于点G,然后根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,再根据∠GFC+∠FGC+∠C=180°,可得x=∠A+∠B+∠C+∠D+∠E=180°,据此解答即可.
(3)根据∠BOD=70°,可得∠A+∠C+∠E=70°,∠B+∠D+∠F=70°,据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可.
(1)证明:如图,延长BO交AC于点D,则∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)180;180;180
(3)140
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?

-
科目: 来源: 题型:
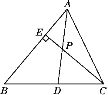
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD、CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明的手机没电了,现有一个只含A,B,C,D四个同型号插座的插线板(如图,假设每个插座都适合所有的充电插头,且被选中的可能性相同),请计算:

(1)若小明随机选择一个插座插入,则插入A的概率为;
(2)现小明对手机和学习机两种电器充电,请用列表或画树状图的方法表示出两个插头插入插座的所有可能情况,并计算两个插头插在相邻插座的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点P是BC的中点,仅用无刻度的直尺按要求画图:
(1)在图①中画出AD的中点M;
(2)在图②中画出对角线AC的三等分点E,点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0,
(1)当k为何值时,方程有实数根;
(2)设x1 , x2是方程的两个实数根,且x12+x22=4,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点A,B,E在x轴上.

(1)若点F的坐标为(6,3),直接写出点C和点A的坐标;
(2)若正方形BEFG的边长为6,求点C的坐标.
相关试题

