【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象
的图象![]() 分别与
分别与![]() ,
,![]() 轴交于
轴交于![]() ,
,![]() 两点,正比例函数的图象
两点,正比例函数的图象![]() 与
与![]() 交于点
交于点![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)4
;(2)4![]() ;(3)
;(3)![]() 或2或
或2或![]() .
.
【解析】
(1)先求得点![]() 的坐标,再运用待定系数法即可得到
的坐标,再运用待定系数法即可得到![]() 的解析式;
的解析式;
(2)过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,则
,则![]() ,
,![]() ,再根据
,再根据![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,进而得出
,进而得出![]() 的值;
的值;
(3)分三种情况:当![]() 经过点
经过点![]() 时,
时,![]() ;当
;当![]() ,
,![]() 平行时,
平行时,![]() ;当
;当![]() ,
,![]() 平行时,
平行时,![]() ;故
;故![]() 的值为
的值为![]() 或2或
或2或![]() .
.
解:(1)把![]() 代入一次函数
代入一次函数![]() ,可得
,可得
![]() ,
,
解得![]() ,
,
![]() ,
,
设![]() 的解析式为
的解析式为![]() ,则
,则![]() ,
,
解得![]() ,
,
![]() 的解析式为
的解析式为![]() ;
;
(2)如图,过![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,则
,则![]() ,
,![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;

(3)一次函数![]() 的图象为
的图象为![]() ,且
,且![]() ,
,![]() ,
,![]() 不能围成三角形,
不能围成三角形,
![]() 当
当![]() 经过点
经过点![]() 时,
时,![]() ;
;
当![]() ,
,![]() 平行时,
平行时,![]() ;
;
当![]() ,
,![]() 平行时,
平行时,![]() ;
;
故![]() 的值为
的值为![]() 或2或
或2或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家文化用品商场平时以同样价格出售相同的商品.六一期间两家商场都让利酬宾,其中甲商场所有商品一律按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)分别写出两家商场购物金额
 (元)与商品原价
(元)与商品原价 (元)的函数解析式;
(元)的函数解析式;(2)在如图所示的直角坐标系中画出(1)中函数的图象;
(3)六一期间如何选择这两家商场购物更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
 是正方形,
是正方形,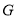 是直线
是直线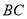 上任意一点,
上任意一点,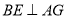 于点
于点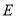 ,
,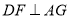 于点
于点 .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.
(1)当点
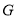 在
在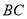 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出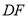 、
、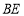 、
、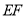 的数量关系,并证明;
的数量关系,并证明;(2)当点
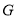 在
在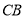 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出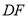 、
、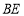 、
、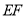 的数量关系,不用证明.
的数量关系,不用证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=
 ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用
 (元)与种植面积
(元)与种植面积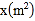 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当
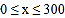 和
和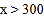 时,
时, 与
与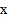 的函数关系式;
的函数关系式;(2)广场上甲、乙两种花卉的种植面积共
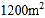 ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于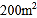 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
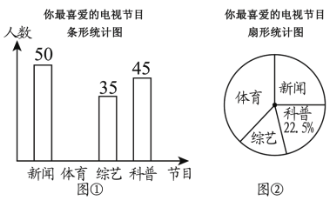
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为
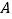 ),“体育节目”(记为
),“体育节目”(记为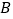 ),“综艺节目”(记为
),“综艺节目”(记为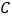 ),“科普节目”(记为
),“科普节目”(记为 )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“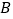 ”和“
”和“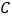 ”两位观众的概率.
”两位观众的概率.
相关试题

