【题目】20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准偏差 | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐与最轻的一筐相差多少千克?
(2)这20筐白菜的平均质量比标准质量多或少多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
参考答案:
【答案】(1)5.5千克(2)0.4千克(3)1016元
【解析】
(1)根据最大数减最小数,即可得出答案;
(2)根据有理数的加法,可得实际质量,然后除以总数即可得出平均质量,最后根据有理数的大小比较即可得出答案;
(3)根据有理数的乘法先算出20筐标准质量的总重量,然后加上多出的8千克,即可得出总重量,然后根据单价乘以数量,即可得出答案.
解:(1)2.5-(-3)=5.5千克,
(2)![]() 千克,
千克,![]() 千克,
千克,
(3)![]() 千克,
千克,![]() 元,
元,
答:最重的一筐与最轻的一筐相差5.5千克,这20筐白菜的平均质量比标准质量多0.4千克出售这20筐白菜可卖1016元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司购买了办公用的A、B两种型号护眼台灯共60盏,花费了 5160元.已知A型台灯每盏80元,B型台灯每盏100元.则A、B两种型号的护 眼台灯各买了多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技有限公司准备购进A和B两种机器人来搬运化工材料,已知购进A种机器人2个和B种机器人3个共需16万元,购进A种机器人3个和B种机器人2个共需14万元,请解答下列问题:
(1)求A、B两种机器人每个的进价;
(2)已知该公司购买B种机器人的个数比购买A种机器人的个数的2倍多4个,如果需要购买A、B两种机器人的总个数不少于28个,且该公司购买的A、B两种机器人的总费用不超过106万元,那么该公司有哪几种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20箱橘子,以每箱25kg为标准,超过或不足的千克数分别用正,负数来表示:记录如下:
与标准质量的差值(kg)
-3
-2
-1.5
0
1
2.5
箱数
1
4
2
3
2
8
(1)与标准重量比较,这20箱橘子总计超过或不足多少千克?
(2)若橘子每千克售价2.5元,则出售这20箱橘子可卖多少元?
-
科目: 来源: 题型:
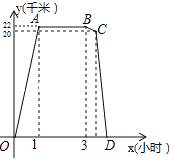
查看答案和解析>>【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE的中点,连接CF,DF.

(1)如图1,当点D在AB上,点E在AC上时
①证明:△BFC是等腰三角形;
②请判断线段CF,DF的关系?并说明理由;
(2)如图2,将图1中的△ADE绕点A旋转到图2位置时,请判断(1)中②的结论是否仍然成立?并证明你的判断.
相关试题

