【题目】已知:如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G. 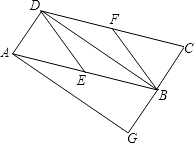
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE= ![]() AB,CF=
AB,CF= ![]() CD.
CD.
∴AE=CF.
在△AED和△CBF中,
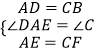 ,
,
∴△ADE≌△CBF(SAS)
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴四边形AGBD是矩形.
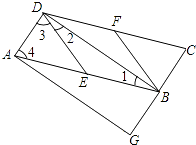
【解析】(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
【考点精析】根据题目的已知条件,利用平行四边形的性质和菱形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
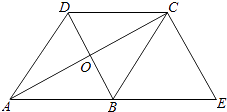
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】若设a>b>0,用“>”、“<”填空:①3a____b,②-4a____4b,则下列选项中,填空正确的是( )
A. >,> B. >,< C. <,< D. <,>
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的周长为10,它的长是a,那么它的宽是( )
A.10﹣a
B.10﹣2a
C.5﹣a
D.5﹣2a -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.

(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式及其验证过程: 验证:
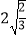 =
= 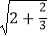 ;
;
验证: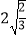 =
= 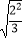 =
= 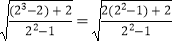 =
= 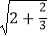 ;
;
验证: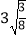 =
= 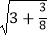 ;
;
验证: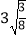 =
= 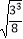 =
= 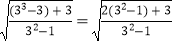 =
= 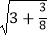 .
.
(1)按照上述两个等式及其验证过程的基本思路,猜想4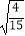 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B、C在同一条直线上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点.
(1)画出符合题意的图形;
(2)依据(1)的图形,求线段MN的长.
相关试题

