【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE. 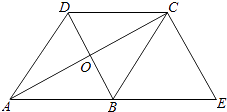
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
参考答案:
【答案】
(1)证明:∵菱形ABCD,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形,
∴BD=EC
(2)解:∵平行四边形BECD,
∴BD∥CE,
∴∠ABO=∠E=50°,
又∵菱形ABCD,
∴AC丄BD,
∴∠BAO=90°﹣∠ABO=40°
【解析】(1)根据菱形的对边平行且相等可得AB=CD,AB∥CD,然后证明得到BE=CD,BE∥CD,从而证明四边形BECD是平行四边形,再根据平行四边形的对边相等即可得证;(2)根据两直线平行,同位角相等求出∠ABO的度数,再根据菱形的对角线互相垂直可得AC⊥BD,然后根据直角三角形两锐角互余计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分为四类(A.特别好,B.好,C.一般,D.较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:
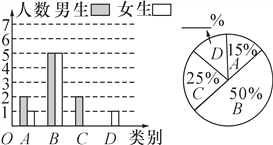
(1)本次调查中,王老师一共调查了________名学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)假定全校各班实施新课程改革效果一样,全校共有学生2400人,请估计该校新课程改革效果达到A类的有多少学生;
(4)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当-ax<ay,x>-y,则a的值为( )
A. a=0 B. a<0 C. a>0 D. 任意有理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2、﹣2、4、1、0的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若设a>b>0,用“>”、“<”填空:①3a____b,②-4a____4b,则下列选项中,填空正确的是( )
A. >,> B. >,< C. <,< D. <,>
-
科目: 来源: 题型:
查看答案和解析>>【题目】长方形的周长为10,它的长是a,那么它的宽是( )
A.10﹣a
B.10﹣2a
C.5﹣a
D.5﹣2a -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
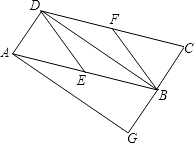
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
相关试题

