【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
参考答案:
【答案】D
【解析】由图象对称轴为直线x=-![]() ,则-
,则-![]() =-
=-![]() ,得a=b,
,得a=b,
A中,由图象开口向上,得a>0,则b=a>0,由抛物线与y轴交于负半轴,则c<0,则abc<0,故A错误;
B中,由a=b,则a-b=0,故B错误;
C中,由图可知当x=1时,y<0,即a+b+c<0,又a=b,则2b+c<0,故C错误;
D中,由抛物线的对称性,可知当x=1和x=-2时,函数值相等,则当x=-2时,y<0,即4a-2b+c<0,则4a+c<2b,故D正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣
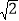 与 是关于1的平衡数;
与 是关于1的平衡数;(2)若(m+
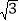 )×(1﹣
)×(1﹣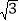 )=﹣5+3
)=﹣5+3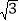 ,判断m+
,判断m+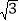 与5﹣
与5﹣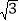 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的是( )

A. 甲队率先到达终点 B. 甲队比乙队多走了200米路程
C. 乙队比甲队少用0.2分钟 D. 比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线y=x2+bx﹣c经过直线y=x﹣3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)求S△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车
乙型客车
载客量(人/辆)
35
30
租金(元/辆)
400
320
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?
相关试题

