【题目】(1)如图(1),已知任意三角形ABC,过点C作DE∥AB;
①求证:∠DCA=∠A; ②求证:∠A+∠B+∠ACB=180°;
(2)如图(2),求证:∠AGF=∠AEF+∠F;
(3)如图(3),AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.

参考答案:
【答案】(1)证明见解析;(2)证明见解析(3)29.5°.
【解析】分析:(1)①根据“两直线平行,内错角相等”可证明;②结合①的证明,转化为平角的意义证明三角形的内角和;
(2)根据平角的意义和三角形的内角和,等量代换即可;
(3)先根据两直线平行,内错角相等,同旁内角互补,求得∠AED和∠DEB的度数,再根据平角的意义和角平分线的性质求得∠DEF的度数,结合(2)的结论可求解.
详解:证明:(1)①∵DE∥BC,∴∠DCA=∠A;
②如图1所示,在△ABC中,∵DE∥BC,
∴∠B=∠ECA,∠DCA=∠A(内错角相等).
∵∠ECA+∠BCA+∠DCA=180°,
∴∠A+∠B+∠C=180°.
即三角形的内角和为180°;
(2)∵∠AGF+∠FGE=180°,
由(1)知,∠GEF+∠F+∠FGE=180°,
∴∠AGF=∠AEF+∠F;
(3)∵AB∥CD,∠CDE=119°,
∴∠DEB=119°,∠AED=61°,
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=59.5°,
∴∠AEF=120.5°,
∵∠AGF=150°,
∵∠AGF=∠AEF+∠F,
∴∠F=150°﹣120.5°=29.5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间
 (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类:  类(
类( ),
), 类(
类( ),
), 类(
类( ),
), 类(
类( ),
), 类(
类( ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.
根据以上信息,解答下列问题:
(1)
 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;(2)
 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;(3)从该班做义工时间在
 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在 中的概率.
中的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是
 ”,小明做了下列三个模拟实验来验证.
”,小明做了下列三个模拟实验来验证.①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值;
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,计算指针落在奇数区域的次数与总次数的比值;
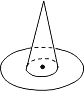
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值. 上面的实验中,不科学的有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】同底数幂相乘,____________不变,____________相加,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的面积为1.分别倍长(延长一倍)
的面积为1.分别倍长(延长一倍) ,BC,CA得到
,BC,CA得到 .再分别倍长A1B1,B1C1,C1A1得到
.再分别倍长A1B1,B1C1,C1A1得到 .…… 按此规律,倍长2018次后得到的
.…… 按此规律,倍长2018次后得到的 的面积为( )
的面积为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为验证“掷一个质地均匀的骰子,向上的点数为偶数的概率是0.5”,下列模拟实验中,不科学的是( )
A. 袋中装有1个红球一个绿球,它们除颜色外都相同,计算随机摸出红球的概率
B. 用计算器随机地取不大于10的正整数,计算取得奇数的概率
C. 随机掷一枚质地均匀的硬币,计算正面朝上的概率
D. 如图,将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形,转动转盘任其自由停止,计算指针指向甲的概率

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列对于三角形一边上的高的说法中正确的是( )
A.必在三角形内部B.必在三角形外部
C.必与三角形的一边重合D.以上三种情况都有可能
相关试题

