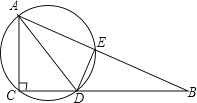
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD外接圆的直径.
参考答案:
【答案】(1)证明见解析;(2)3![]()
【解析】试题分析:(1)由Rt△ABC中,∠ACB=90°,可得AD是直径,可得△ADE为直角三角形,在两个直角三角形中,利用AAS可得两三角形全等,得到答案;
(2)先根据勾股定理求出AB的长,由(1)知,AC=AE,CD=DE,设CD=x,则BD=8-x,在Rt△BDE中,根据勾股定理求出x的值,同理,在Rt∠ACD中求出AD的长,进而可得出结论.
试题解析:
(1)证明:∵Rt△ABC中,∠ACB=90°,
∴AD为圆的直径,
∴∠AED=90°,
∵AD是△BAC的∠CAB的角平分线,
∴∠CAD=∠EAD,
Rt△ACD与Rt△ADE中,
∠CAD=∠BAD, ∠ACB=∠AED ,AD=AD ,
∴Rt△ACD≌Rt△ADE(AAS),
∴AC=AE.
(2)∵在Rt△ABC中,∠ACB=90°,AC=6,CB=8,
∴![]()
∵由(1)知,AC=AE,CD=DE,∠ACD=∠AED=90°,
∴设CD=x,则BD=8-x,BE=AB-AE=10-6=4,
在Rt△BDE中, ![]()
![]() ,即
,即![]()
![]() 解得x=3.
解得x=3.
在Rt△ACD中![]()
![]() 即
即![]() 解得AD=
解得AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果
 ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )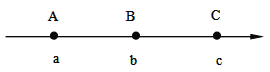
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.若AF=3,tan∠ABD=
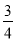 ,求⊙O的直径.
,求⊙O的直径.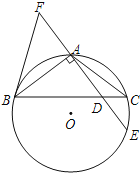
-
科目: 来源: 题型:
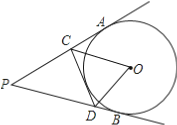
查看答案和解析>>【题目】如图,P为⊙O外一点,PA,PB分别切⊙O于A,B,CD切⊙O于点E,分别交PA,PB于点C,D.若PA=5,则△PCD的周长和∠COD分别为( )
A. 5,
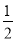 (90°+∠P) B. 7,90°+
(90°+∠P) B. 7,90°+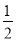 C. 10,90°-
C. 10,90°-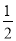 ∠P D. 10,90°+
∠P D. 10,90°+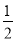 ∠P
∠P -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为 ______
DM=BD+BE=4cm+4cm=8cm,
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,一条生产线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A1,A2,A3,A4,A5表示.
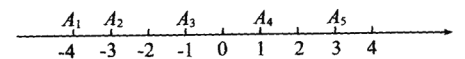
(1)若原点是零件的供应点,5个机器人分别到供应点取货的总路程是多少?
(2)若将零件的供应点改在A1,A3,A5中的其中一处,并使得5个机器人分别到达供应点取货的总路程最短,你认为应该在哪个点上?通过计算说明理由.
相关试题

