【题目】如图已知数轴上点A、B分别表示a、b,且|b+6|与(a﹣9)2互为相反数,O为原点.
(1)a= ,b= ;
(2)若将数轴折叠点A与表示﹣10的点重合,则与点B重合的点所表示的数为 ;
(3)若点M、N分别从点A、B同时出发,点M以每秒1个单位长度的速度沿数轴向左匀速运动,点N以每秒2个单位长度的速度沿数轴向右匀速运动,N到点A后立刻原速返回,设运动时间为t(t>0)秒.①点M表示的数是 (用含t的代数式表示);②求t为何值时,2MO=MA;③求t为何值时,点M与N相距3个单位长度.
![]()
参考答案:
【答案】(1)a=9,b=﹣6;(2)与点B重合的点所表示的数为5;(3)①点M表示的数是9﹣t;②
t为4或6或12或18秒时,点M与N相距3个单位长度.
【解析】
(1)根据非负数的性质即可求解;
(2)先求出折叠点,依此可求与点B重合的点所表示的数;
(3)①根据路程=速度×时间可求点M表示的数;
②分M在原点右边和原点左边两种情况进行讨论可求t的值;
③分点M与N第一次相遇前后,点M与N第二次相遇前后,进行讨论可求t的值.
解:(1)依题意有|b+6|+(a﹣9)2=0,
b+6=0,a﹣9=0,
解得a=9,b=﹣6;
(2)(9﹣10)÷2=﹣0.5,
﹣0.5+6=5.5,
﹣0.5+5.5=5.
故与点B重合的点所表示的数为5;
(3)①点M表示的数是9﹣t;
②M在原点右边时,
依题意有2(9﹣t)=t,解得t=6;
M在原点左边边时,
依题意有﹣2(9﹣t)=t,解得t=18.
故t为6或18秒时,2MO=MA;
③点M与N第一次相遇前,
依题意有3t=15﹣3,
解得t=4;
点M与N第一次相遇后,
依题意有3t=15+3,
解得t=6;
(6+9)÷2=7.5(秒),
点M与N第二次相遇前,
2(t﹣7.5)﹣(t﹣7.5)=7.5﹣3,
解得t=12;
点M与N第二次相遇后,
2(t﹣7.5)﹣(t﹣7.5)=7.5+3,
解得t=18.
故t为4或6或12或18秒时,点M与N相距3个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板拼成如图所示的图形,即
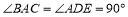 ,
, ,
, ,
,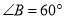 ,
,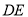 与
与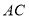 相交于点
相交于点 .
.

(1)如果
 ,那么
,那么 与
与 平行吗?试说明理由;
平行吗?试说明理由;(2)将
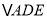 绕着点
绕着点 逆时针旋转,使得点
逆时针旋转,使得点 落在边
落在边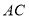 上,联结
上,联结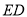 并延长交
并延长交 于点
于点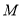 ,联结
,联结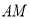 ,若
,若 ,
, ,
, ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:(﹣2)﹣1﹣(2017﹣π)0+sin30°;
(2)化简: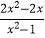 ﹣
﹣ 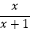 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)为倡导节约用电,某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)(4分)小张家2015年2月份用电100千瓦时,上缴电费68元;3月份用电120千瓦时,上缴电费88元.问“基本电价”和“提高电价”分别为多少元/千瓦时?
(2)(3分)若4月份小张家预计用电130千瓦时,请预算小张家4月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两图的网格都是由边长为1的小正方形组成,我们把顶点在正方形顶点的三角形称为格点三角形.
(1)求图①中格点△ABC的周长和面积;
(2)在图②中画出格点△DEF,使它的边长满足DE=2
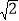 ,DF=5,EF=
,DF=5,EF=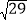 ,并求出△DEF的面积.
,并求出△DEF的面积.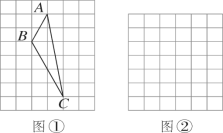
-
科目: 来源: 题型:
查看答案和解析>>【题目】某调查公司对本区域的共享单车数量及使用次数进行了调查发现,今年3月份第1周共有各类单车1000辆,第2周比第1周增加了10%,第3周比第2周增加了100辆.
调查还发现某款单车深受群众喜爱,第1周该单车的每辆平均使用次数是这一周所有单车平均使用次数的2.5倍,第2周、第3周该单车的每辆平均使用次数都比前一周增长一个相同的百分数m,第3周所有单车的每辆平均使用次数比第1周增加的百分数也是m,而且第3周该款单车(共100辆)的总使用次数占到所有单车总使用次数的四分之一(注:总使用次数=每辆平均使用次数×车辆数).
(1)求第3周该区域内各类共享单车的总数量;
(2)求m的值.
相关试题

