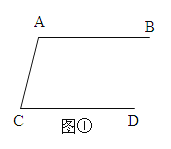
【题目】(1)如图①,AB∥CD,那么∠A+∠C= 度
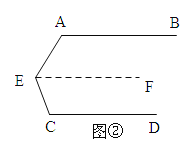
(2)如图②,AB∥CD∥EF,那么∠A+∠AEC+∠C= 度
(3)如图③,AB∥GH∥MN∥CD,那么∠A+∠AGM+∠GMC+∠C=度,并说明理由。

参考答案:
【答案】(1)180;(2)360;(3) 540,理由见解析.
【解析】
(1)根据两直线平行,同旁内角互补即可求得;
(2)两次运用两直线平行,同旁内角互补即可求得;
(3)与(2)相同,利用同旁内角互补即可求得.
解:(1)根据两直线平行,同旁内角互补即可求得:∠A+∠C=180°;
(2)∵EF∥AB,
∴∠A+∠AEF=180°( 两直线平行,同旁内角互补).
∵AB∥CD( 已知),EF∥AB,
∴EF∥CD)
∴∠C+∠CEF=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C=360°
即∠A+∠AEC+∠C=360°;
(3)同(2)可得:∠A+∠AGH+∠HGM+∠GMN+∠NMC+∠C=540°,
即∠A+∠AGM+∠GMC+∠C=540°.
故答案为:180,360,540.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).

(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月)
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,
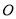 为坐标原点,点
为坐标原点,点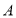 的坐标为
的坐标为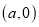 ,点
,点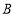 的坐标为
的坐标为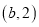 ,点
,点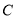 的坐标为
的坐标为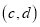 ,其中
,其中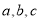 满足方程组
满足方程组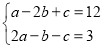 .
.(1)若点
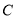 到
到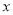 轴的距离为6,则
轴的距离为6,则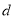 的值为_________;
的值为_________;(2)连接
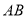 ,线段
,线段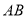 沿
沿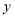 轴方向向上平移到线段
轴方向向上平移到线段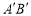 ,则点
,则点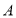 到直线
到直线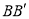 的距离为_______,线段
的距离为_______,线段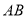 扫过的面积为15,则点
扫过的面积为15,则点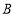 平移后对应点
平移后对应点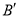 的纵坐标为_______;
的纵坐标为_______;(3)连接
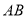 ,
,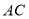 ,
,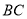 ,若
,若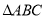 的面积小于等于12,求
的面积小于等于12,求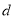 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

-
科目: 来源: 题型:
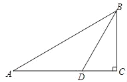
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
相关试题

