【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0)、B(4,﹣1)、C(3,2).
(1)在所给的直角坐标系中画出△ABC;
(2)把△ABC向左平移3个单位,再向上平移2个单位得到△A′B′C′,画出△A′B′C′并写出点C′的坐标;
(3)求△A′B′C′的面积.

参考答案:
【答案】(1)画图见解析;(2)画图见解析,点C′的坐标为:(0,4);(3)△A′B′C′的面积为7.
【解析】
(1)根据网格结构找出点A、B、C的位置,然后顺次连接即可; (2)根据网格结构找出点A、B、C向左平移3个单位,再向上平移2个单位后对应点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标; (3)根据三角形的面积公式列式计算即可得解.
(1)如图所示:△ABC,即为所求;
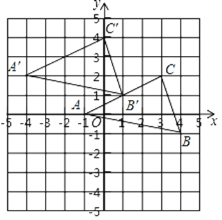
(2)如图所示:△A′B′C′即为所求,点C′的坐标为:(0,4);
(3)△A′B′C′的面积为:5×3﹣![]() ×1×3﹣
×1×3﹣![]() ×2×4﹣
×2×4﹣![]() ×1×5=7.
×1×5=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,
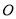 为坐标原点,点
为坐标原点,点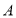 的坐标为
的坐标为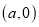 ,点
,点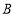 的坐标为
的坐标为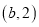 ,点
,点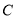 的坐标为
的坐标为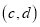 ,其中
,其中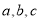 满足方程组
满足方程组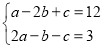 .
.(1)若点
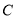 到
到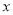 轴的距离为6,则
轴的距离为6,则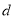 的值为_________;
的值为_________;(2)连接
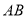 ,线段
,线段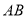 沿
沿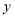 轴方向向上平移到线段
轴方向向上平移到线段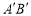 ,则点
,则点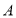 到直线
到直线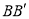 的距离为_______,线段
的距离为_______,线段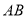 扫过的面积为15,则点
扫过的面积为15,则点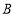 平移后对应点
平移后对应点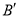 的纵坐标为_______;
的纵坐标为_______;(3)连接
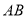 ,
,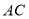 ,
,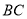 ,若
,若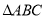 的面积小于等于12,求
的面积小于等于12,求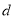 的取值范围.
的取值范围. -
科目: 来源: 题型:
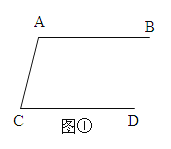
查看答案和解析>>【题目】(1)如图①,AB∥CD,那么∠A+∠C= 度
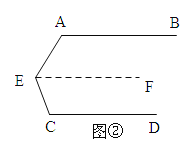
(2)如图②,AB∥CD∥EF,那么∠A+∠AEC+∠C= 度
(3)如图③,AB∥GH∥MN∥CD,那么∠A+∠AGM+∠GMC+∠C=度,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

-
科目: 来源: 题型:
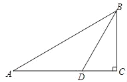
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
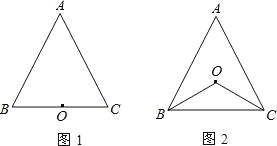
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律: ①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本)
相关试题

