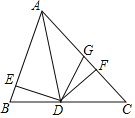
【题目】如图,已知AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BD=DG.
下列结论:(1)DE=DF;(2)∠B=∠DGF; (3)AB<AF+FG;(4)若△ABD和△ADG的面积分别是50和38,则△DFG的面积是8.其中一定正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】B
【解析】
(1)根据角平分线的性质可得出DE=DF,结论(1)正确;
(2)由DE=DF、∠BED=∠GFD、BD=GD可证出△BDE≌△GDF(HL),根据全等三角形的性质可得出∠B=∠DGF,结论(2)正确;
(3)利用全等三角形的判定定理AAS可证出△ADE≌△ADF,由此可得出AE=AF,根据△BDE≌△GDF可得出BE=GF,结合AB=AE+EB即可得出AB=AF+FG,结论(3)不正确;
(4)根据全等三角形的性质可得出S△ADE=S△ADF、S△BDE=S△GDF,结合S△ABD=S△ADE+S△BDE=50、S△ADG=S△ADF-S△GDF=38可求出△DFG的面积是6,结论(4)不正确.综上即可得出结论.
(1)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,结论(1)正确;
(2)在△BDE和△GDF中,![]() ,
,![]()
∴△BDE≌△GDF(HL),
∴∠B=∠DGF,结论(2)正确;
(3)在△ADE和△ADF中,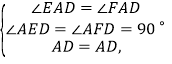
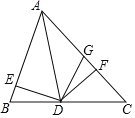
∴△ADE≌△ADF(AAS),
∴AE=AF.
∵△BDE≌△GDF,
∴BE=GF,
∴AB=AE+EB=AF+FG,结论(3)不正确;
(4)∵△ADE≌△ADF,△BDE≌△GDF,
∴![]()
∵![]()
∴![]() ,结论(4)不正确。
,结论(4)不正确。
综上所述:正确的结论有(1)(2).
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:
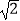 =1.41,
=1.41, 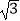 =1.73)
=1.73) 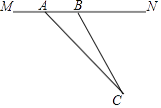
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则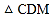 周长的最小值为
周长的最小值为


A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x与反比例函数y=
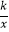 (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=  .
. 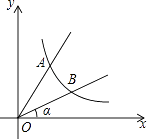
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.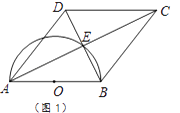
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求弧AE的长.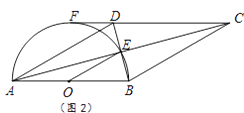
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列三行数,并完成后面的问题:
①-2,4,-8,16,……
②1,-2,4,-8,……
③0,-3,3,-9,……
(1)思考第①行数的规律,写出第
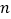 个数字是________;
个数字是________;(2)设第②行第
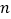 个数为
个数为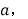 第③行第
第③行第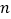 个数为
个数为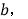 请直接写出
请直接写出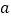 与
与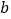 之间的关系;
之间的关系;(3)设
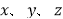 分别表示第①、②、③行数的第2019个数字,求
分别表示第①、②、③行数的第2019个数字,求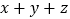 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

相关试题

