【题目】动手操作:
(1)如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD= 度;
(2)如图2,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
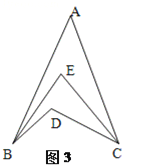
(3)灵活应用:请你直接利用以上结论,解决以下列问题:如图3,BE平分∠ABD,CE平分∠ACD,若∠BAC=40°,∠BDC=120°,求∠BEC的度数。



参考答案:
【答案】(1)60°;(2)猜想:∠A+∠B+∠C=∠BDC ,证明见解析;(3)∠BEC=80°;
【解析】试题分析:(1)在△BDC中,由三角形内角和定理可得∠DBC+∠DCB=90°,再由∠ABC+∠ACB=150°,从而可得;
(2)连接BC,利用三角形内角和定理推导即可得;
(3)由(2)可知∠A+∠ABD+∠ACD=∠BDC,∠A+∠ABE+∠ACE=∠BEC,再根据角平分线的定义即可得.
试题解析:(1)60°;
(2)猜想:∠A+∠B+∠C=∠BDC ;
证明如下:连接BC,
在△DBC中,∵∠DBC+∠DCB+∠D=180°,
∴∠DBC+∠DCB=180°﹣∠BDC;
在Rt△ABC中,
∵∠ABC+∠ACB+∠A=180°,
即∠ABD+∠DBC+∠DCB+∠ACD+∠A=180°,
而∠DBC+∠DCB=180°﹣∠BDC,
∴∠A+∠ABD+∠ACD=180°﹣(180°﹣∠BDC)=∠BDC,
即:∠A+∠B+∠C=∠BDC.
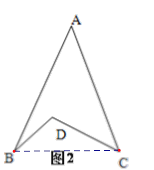
(3)灵活应用:
由(2)可知∠A+∠ABD+∠ACD=∠BDC,∠A+∠ABE+∠ACE=∠BEC,
∵∠BAC=40°,∠BDC=120°,
∴∠ABD+∠ACD=120°﹣40°=80°
∵BE平分∠ABD,CE平分∠ACB,
∴∠ABE+∠ACE=40°,
∴∠BEC=40°+40°=80°;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. a12÷a6=a6B. (a﹣2b)2=a﹣4b
C. a3a3=2a6D. (a2)3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABD和△ACE中,有下列判断:
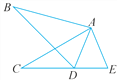
①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(-12.56)+(-7.25)+3.01+(-10.01)+7.25;
(2)0.47+(-0.09)+0.39+(-0.3)+1.53;
(3)
 ;
;(4)23+(-72)+(-22)+57+(-16);
(5)
 ;
;(6)2.25+(-4
 )+(-2.5)+2
)+(-2.5)+2 +3.4+(-
+3.4+(- )
)(7)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
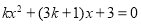
 。
。(1)求证:无论k取何值,方程总有两个实数根;
(2)若二次函数
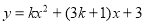 的图象与
的图象与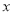 轴两个交点的横坐标均为整数,且k为整数,求k的值。(本题10分)
轴两个交点的横坐标均为整数,且k为整数,求k的值。(本题10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.

(1)两个变量中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(填<、=、或>);
(3)路程为150km时,甲行驶了 小时,乙行驶了 小时.
(4)甲比乙先走了 小时;在9时, 走在前面。
相关试题

