【题目】如图，在△ABD和△ACE中，有下列判断：

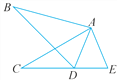
①AB＝AC；②∠B＝∠C；③∠BAC＝∠EAD；④AD＝AE.

请用其中的三个判断作为条件，余下的一个判断作为结论(用序号的形式)，写出一个由三个条件能推出结论成立的式子，并说明理由．

参考答案：

【答案】证明见解析

【解析】试题分析：

按题中要求，选3个作条件，1个作结论，则有：（1）① ② ③ ④ ；（2）①②④③；（3）①③④②；（4）②③④①；共计四种组合方式.然后根据全等三角形的判定方法，可知其中（2）不能判定△ABD≌△ACE，从而不能得到结论，其余的三种组合都可以通过证△ABD≌△ACE而得到结论，故有三种组合方式是成立的，我们选择其中一个进行证明即可.

试题解析：

（1）有三种组合是成立的：① ② ③④ 或①③④② 或②③④①.

（2）如①②③④ 理由如下：

∵∠BAC＝∠EAD，

∴∠BAC+∠CAD＝∠EAD+∠CAD，即∠BAD＝∠CAE，

∴在△ABD和△ACE中： ，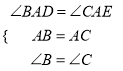

∴△ABD≌△ACE(ASA)．

∴ AD＝AE.

关闭