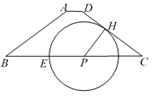
【题目】如图,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.
(1)当圆P过点A时,求圆P的半径;
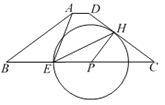
(2)分别联结EH和EA,当△ABE∽△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;
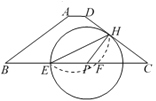
(3)将劣弧![]() 沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
参考答案:
【答案】(1)圆P的半径长为3;(2)![]() ;(3)说明见解析,
;(3)说明见解析,![]() .
.
【解析】分析:
(1)如下图,作AM⊥BC于M,联结AP,由题意易得AM=3,BM=4,tanB=tanC=![]() ,设PH=3k,则可得HC=4k,CP=5k,MP=5-5k,在Rt△APM中,由勾股定理可得
,设PH=3k,则可得HC=4k,CP=5k,MP=5-5k,在Rt△APM中,由勾股定理可得![]() ,结合AP=PH即可列出关于k的方程,解方程即可求得k的值,再结合CP<BC检验即可得到所求答案;
,结合AP=PH即可列出关于k的方程,解方程即可求得k的值,再结合CP<BC检验即可得到所求答案;
(2)由(1)可知,若设PH=3k,则HC=4k,CP=5k,由点E在圆P上可得PE=3k,CE=8k,BE=9-8k,由△ABE∽△CEH可得 ![]() ,由此可得:
,由此可得:![]() ,解得k的值即可求得圆P的半径和BE的长,结合圆B和圆P的位置关系是相交,即可求得圆B的半径r的取值范围;
,解得k的值即可求得圆P的半径和BE的长,结合圆B和圆P的位置关系是相交,即可求得圆B的半径r的取值范围;
(3)在圆P上取点F关于EH对称的点G,联结EG,作PQ⊥EG于G,HN⊥BC于N,
则EG=EF,∠1=∠3,EQ=QG,EF=EG=2EQ. 结合已知条件先证△EPQ≌△PHN可得EQ=PN,从而可得EF=EG=2PN,由(1)可知,在Rt△PHC中,若设PH=3k,则HC=4k,PC=5k,由此可得sinC=![]() ,cosC=
,cosC=![]() ,在Rt△CHN中由此可把HN、NC用含k的式子表达出来,进一步可把PN、EN用含k的式子表达出来,这样就可把EH和EF用含k的代数式表达出来,由此即可求得EH和EF的比值,得到相应的结论.
,在Rt△CHN中由此可把HN、NC用含k的式子表达出来,进一步可把PN、EN用含k的式子表达出来,这样就可把EH和EF用含k的代数式表达出来,由此即可求得EH和EF的比值,得到相应的结论.
详解:
(1)作AM⊥BC于M,联结AP,
∵梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,
∴BM=(BC-AD)÷2=4,AM=![]() ,
,
∴tanB= tanC=![]() ,
,
∵PH⊥DC,
∴若设PH=3k,则HC=4k,CP=5k.
∵BC=9,
∴MP=5-5k.
∴![]() ,
,
∵AP=PH,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
当![]() 时,CP=
时,CP=![]() ,
,
∴![]() (舍去),
(舍去),
∴![]() ,
,
∴圆P的半径长为3;

(2)由(1)可知,若设PH=3k,则HC=4k,CP=5k.
∵点E在圆P上,
∴PE=3k,CE=8k,
∴BE=9-8k,
∵△ABE∽△CEH,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() ,即圆P的半径为
,即圆P的半径为![]() ,
,
∵圆B与圆P相交,又BE=9-8k=![]() ,
,
∴![]() ;
;

(3)在圆P上取点F关于EH对称的点G,联结EG,作PQ⊥EG于G,HN⊥BC于N,
则EG=EF,∠1=∠3,EQ=QG,EF=EG=2EQ.
∴∠GEP=2∠1,
∵PE=PH,
∴∠1=∠2 ,
∴∠4=∠1+∠2=2∠1,
∴∠GEP=∠4,
∴△EPQ≌△PHN,
∴EQ=PN,
由(1)可知,若设PH=3k,则HC=4k,PC=5k,
∴sinC=![]() ,cosC=
,cosC=![]() ,
,
∴NC=![]() ,NH=
,NH=![]() ,
,
∴PN=![]() ,
,
∴EF=EG=2EQ=2PN=![]() ,EH=
,EH=![]() ,
,
∴![]() ,即线段EH和EF的比值为定值.
,即线段EH和EF的比值为定值.

-
科目: 来源: 题型:
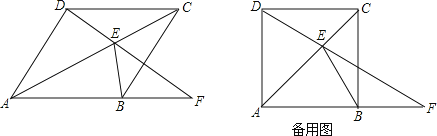
查看答案和解析>>【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车去B地,途经C地休息1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行从B地前往A地.甲、乙两人距A地的路程y(米)与时间x(分)之间的函数关系如图所示,请结合图象解答下列问题:
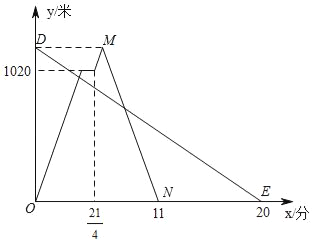
(1)请写出甲的骑行速度为 米/分,点M的坐标为 ;
(2)求甲返回时距A地的路程y与时间x之间的函数关系式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回A地之前,经过多长时间两人距C地的路程相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于点G,连接AG、HG。下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG。其中,正确的结论有( )

A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2019按照一定规律排成下表:
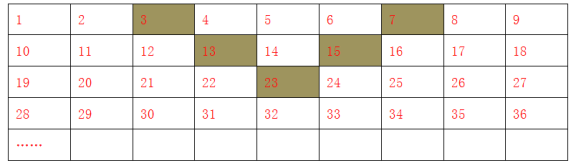
记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a35= ,a54= ;
(2)①若aij=2019,那么i= ,j= ,②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2026.若能, 求出这5个数中的最小数,若不能请说明理由.
-
科目: 来源: 题型:
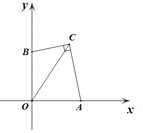
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的值为_________。
相关试题

