【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度,密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:

(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是 (只填上正确答案的序号)
①q=90v+100;②q=![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
参考答案:
【答案】(1)③;(2)v=30时,q达到最大值,q的最大值为1800;(3)①84<k≤96;②流量q最大时d的值为60.
【解析】
试题分析:(1)利用函数的增减性即可判断;
(2)利用配方法,根据二次函数的性质即可解决问题;
(3)①求出v=12或18时,定义的k的值即可解决问题;
②由题意流量q最大时d的值=流量q最大时k的值;
试题解析:(1)函数①q=90v+100,q随v的增大而增大,显然不符合题意.
函数②q=![]() q随v的增大而减小,显然不符合题意.
q随v的增大而减小,显然不符合题意.
故刻画q,v关系最准确的是③.
故答案为:③.
(2)∵![]() =
=![]() ,∵﹣2<0,∴v=30时,q达到最大值,q的最大值为1800.
,∵﹣2<0,∴v=30时,q达到最大值,q的最大值为1800.
(3)①当v=12时,q=1152,此时k=96,当v=18时,q=1512,此时k=84,∴84<k≤96.
②当v=30时,q=1800,此时k=60,∵在理想状态下,假设前后两车车头之间的距离d(米)均相等,∴流量q最大时d的值为60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,计算结果为81﹣x2的是( )
A.(x+9)(x﹣9)
B.(x+9)(﹣x﹣9)
C.(﹣x+9)(﹣x﹣9)
D.(﹣x﹣9)(x﹣9) -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x﹣2017=( )
A. ﹣2017B. ﹣2018C. ﹣2019D. ﹣2020
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.
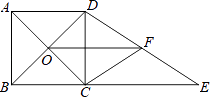
(1)求OF的长.
(2)求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中是二元一次方程的是( )
A.3x+y=0
B.2x﹣1=4
C.2x2﹣y=2
D.2x+y=3z -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a的值.
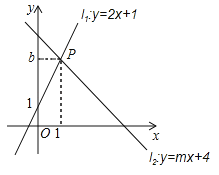
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=kx+b经过点A(﹣30,0)和点B(0,15),直线y=x+5与直线y=kx+b相交于点P,与y轴交于点C.
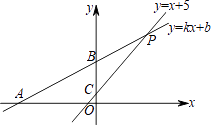
(1)求直线y=kx+b的解析式.
(2)求△PBC的面积.
相关试题

