【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .

参考答案:
【答案】p.
【解析】试题分析:(1)图1,作辅助线构建正方形OECF,设圆O的半径为r,根据切线长定理表示出AD和BD的长,利用AD+BD=5列方程求出半径![]() =1(a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;
=1(a、b是直角边,c为斜边),运用圆面积公式=πr2求出面积=π;
(2)图2,先求斜边上的高CD的长,再由勾股定理求出AD和BD,利用半径![]() (a、b是直角边,c为斜边)求两个圆的半径分别是
(a、b是直角边,c为斜边)求两个圆的半径分别是![]() ,从而求出两圆的面积和=π;
,从而求出两圆的面积和=π;
(3)图3,继续求高DM和CM、BM,利用半径![]() (a、b是直角边,c为斜边)求三个圆的半径分别是
(a、b是直角边,c为斜边)求三个圆的半径分别是![]() ,从而求出三个圆的面积和=π;
,从而求出三个圆的面积和=π;
综上所述:发现S1+S2+S3+…+S10=π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题.
例题:若
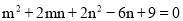 , 求m和n的值
, 求m和n的值解:∵
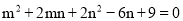
∴
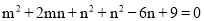
∴
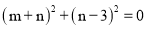
∴
 ,
, 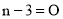
∴
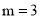 ,
, 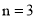
问题:(1)若
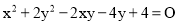 ,求
,求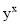 的值.
的值.(2)已知a,b,c是△ABC的三边长,满足
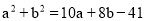 ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.
(1)若AD=2,求AB;
(2)若AB+CD=
 ,求AB.
,求AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC是等边三角形,点P在△ABC内,点Q在△ABC外,分别连接AP、BP、AQ、CQ,∠ABP=∠ACQ, BP=CQ.
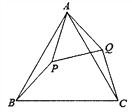
(1)求证:△ABP≌△ACQ;
(2)连接PQ,求证△APQ是等边三角形;
(3)连接P设△CPQ是以
 PQC为顶角的等腰三角形,且∠BPC=100
PQC为顶角的等腰三角形,且∠BPC=100 ,求∠APB的度数.
,求∠APB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

相关试题

