【题目】若一个正整数a可以表示为连续的两个奇数的平方差的形式,如:8=32﹣12,16=52﹣32,24=72﹣52,……,我们则称形如8,16,24这样的正整数a为“奇特数”.
(1)请写出最小的三位“奇特数”,并表示成连续的两个奇数的平方差的形式;
(2)求证:任意一个“奇特数”都是8的倍数;
(3)若一个三位数b为“奇特数”,其百位和个位上的数字相同,十位上的数字比个位上的数字大m(m为正整数),求满足条件的所有三位“奇特数”.
参考答案:
【答案】(1)见解析;(2)见解析;(3)b的值为:232, 464 , 696.
【解析】
新型定义题型,根据题干中奇特数的要求列出式子,在结合因式分解法和平方差公式解决问题,最主要是掌握奇特数是整数这一要素.
(1)解:最小的三位奇特数是:104
104=![]() .
.
(2)证明:设m=![]()
∵m=8k+8, m=8(k+1)
∴r任意一个“奇特数”都是8的倍数
(3)设个位上的数字为:x,则十位数字为:(m+x),百位数字为:x
则b=100x+10(m+x)+x
=100x+10m+10x+x
=111x+10m
∵b为奇特数
∴b是8的倍数![]()
=13x+m+![]() ,
,
又∵![]() 是整数,
是整数,
∴![]() 也是整数且1≤x<10,1≤(x+m)<10,
也是整数且1≤x<10,1≤(x+m)<10,
∴![]() ,
,![]() ,
,![]() (舍),
(舍),![]() ,
,![]() (舍),
(舍),![]() (舍)
(舍)
∴b的值为:232,464,696.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

-
科目: 来源: 题型:
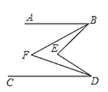
查看答案和解析>>【题目】如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BFD=35°,那么∠BED的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=m (x﹣1)( x﹣4)的图象与x轴交于A,B两点(点A在点B的左边),顶点为C,将该二次函数的图象关于x轴翻折,所得图象的顶点为D.若四边形ACBD为正方形,则m的值为 .
-
科目: 来源: 题型:
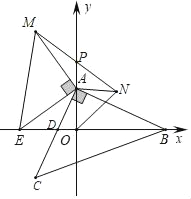
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠CAB=90°,点A,点B的坐标分别为A(0,a),B(b,0),且a,b满足a2+b2﹣4a﹣8b+20=0,AC与x轴交于点D.
(1)求△AOB的面积;
(2)求证:点D为AC的中点;
(3)点E为x轴的负半轴上的动点,分别以OA,AE为直角边在第一、二象限作等腰直角三角形△OAN和等腰直角三角形△EAM,连接MN交y轴于点P,试探究线段OE与AP的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.

(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出不等式组的整数解.
,并写出不等式组的整数解.
相关试题

