【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)由等腰直角三角形的性质和角平分线的性质,可得∠ACB=2∠AEC=45°,可得∠AEC=∠EAC=22.5°,可得AC=EC;
(2)过点D作DM∥AC,交AF的延长线于点M,通过证明△ABE≌△DMA,可得AB=DM,AM=BE,通过证明△ACF≌△MDF,可得BE=AM=2AF.
证明:(1)∵△ABC和△ADE均为等腰直角三角形,
∴AB=AC,AE=AD,∠ACB=∠ABC=∠AED=∠ADE=45°,
∵BE平分∠AED,
∴∠AEB=22.5°
∵∠ACB=∠AEC+∠EAC=45°
∴∠AEC=∠EAC=22.5°
∴AC=EC
(2)如图,过点D作DM∥AC,交AF的延长线于点M,
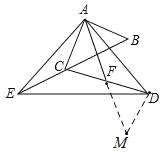
∵∠DAF=∠AEC,且∠AEC+∠EAC=∠ACB=45°
∴∠EAC+∠DAF=45°,且∠DAE=90°,
∴∠CAF=45°
∵AC∥DM,
∴∠CAF=∠DMA=45°
∴∠DMA=∠ABC=45°,且AE=AD,∠AEC=∠DAF,
∴△ABE≌△DMA(AAS)
∴AB=DM,AM=BE,
∴AB=AC=DM,且∠AFC=∠DFM,∠CAF=∠AMD
∴△ACF≌△MDF(AAS)
∴AF=FM
∴AM=2AF=BE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.
(1)第一批脐橙每件进价多少元?
(2)陈老板以每件120元的价格销售第二批脐橙,售出60%后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价﹣进价)
-
科目: 来源: 题型:
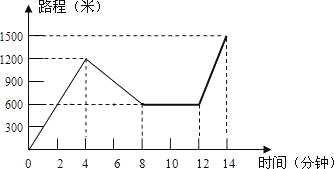
查看答案和解析>>【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
-
科目: 来源: 题型:
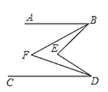
查看答案和解析>>【题目】如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BFD=35°,那么∠BED的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=m (x﹣1)( x﹣4)的图象与x轴交于A,B两点(点A在点B的左边),顶点为C,将该二次函数的图象关于x轴翻折,所得图象的顶点为D.若四边形ACBD为正方形,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正整数a可以表示为连续的两个奇数的平方差的形式,如:8=32﹣12,16=52﹣32,24=72﹣52,……,我们则称形如8,16,24这样的正整数a为“奇特数”.
(1)请写出最小的三位“奇特数”,并表示成连续的两个奇数的平方差的形式;
(2)求证:任意一个“奇特数”都是8的倍数;
(3)若一个三位数b为“奇特数”,其百位和个位上的数字相同,十位上的数字比个位上的数字大m(m为正整数),求满足条件的所有三位“奇特数”.
相关试题

