【题目】已知二次函数y=m (x﹣1)( x﹣4)的图象与x轴交于A,B两点(点A在点B的左边),顶点为C,将该二次函数的图象关于x轴翻折,所得图象的顶点为D.若四边形ACBD为正方形,则m的值为 .
参考答案:
【答案】± ![]()
【解析】解:∵二次函数y=m (x﹣1)( x﹣4)的图象与x轴交于A、B两点,
∴A(1,0),B(4,0),
∴抛物线的对称轴为直线x= ![]() =
= ![]() ,
,
设顶点C的坐标为( ![]() ,a),
,a),
∵四边形ACBD为正方形,
∴|a|= ![]() ,
,
∴C( ![]() ,
, ![]() )或C(
)或C( ![]() ,﹣
,﹣ ![]() ),
),
把C点的坐标代入得, ![]() =m(
=m( ![]() ﹣1)(
﹣1)( ![]() ﹣4)或﹣
﹣4)或﹣ ![]() =m(
=m( ![]() ﹣1)(
﹣1)( ![]() ﹣4),
﹣4),
解得:m= ![]() ,
,
所以答案是:± ![]() .
.
【考点精析】掌握二次函数图象的平移和抛物线与坐标轴的交点是解答本题的根本,需要知道平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
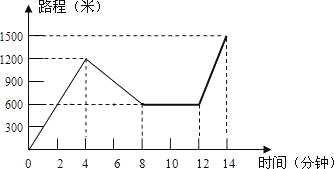
查看答案和解析>>【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

-
科目: 来源: 题型:
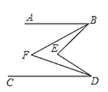
查看答案和解析>>【题目】如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BFD=35°,那么∠BED的度数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正整数a可以表示为连续的两个奇数的平方差的形式,如:8=32﹣12,16=52﹣32,24=72﹣52,……,我们则称形如8,16,24这样的正整数a为“奇特数”.
(1)请写出最小的三位“奇特数”,并表示成连续的两个奇数的平方差的形式;
(2)求证:任意一个“奇特数”都是8的倍数;
(3)若一个三位数b为“奇特数”,其百位和个位上的数字相同,十位上的数字比个位上的数字大m(m为正整数),求满足条件的所有三位“奇特数”.
-
科目: 来源: 题型:
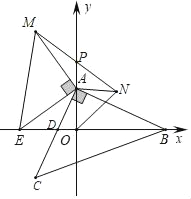
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠CAB=90°,点A,点B的坐标分别为A(0,a),B(b,0),且a,b满足a2+b2﹣4a﹣8b+20=0,AC与x轴交于点D.
(1)求△AOB的面积;
(2)求证:点D为AC的中点;
(3)点E为x轴的负半轴上的动点,分别以OA,AE为直角边在第一、二象限作等腰直角三角形△OAN和等腰直角三角形△EAM,连接MN交y轴于点P,试探究线段OE与AP的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.

(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?
相关试题

