【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

参考答案:
【答案】(1) B(![]() ,2).(2)证明见解析.
,2).(2)证明见解析.
【解析】
试题分析:(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
试题解析:(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=![]() ,
,
∴B(![]() ,2).
,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=![]() NB=ND,
NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则|a+2|-|1-a|=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的腰长为2,则底边a的取值范围是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于作图的语句正确的是( )
A.作∠AOB的平分线OE=3cm
B.画直线AB=线段CD
C.用直尺作三角形的高是尺规作图
D.已知A、B、C三点,过这三点不一定能画出一条直线
-
科目: 来源: 题型:
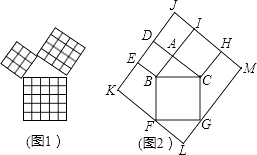
查看答案和解析>>【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.90
B.100
C.110
D.121 -
科目: 来源: 题型:
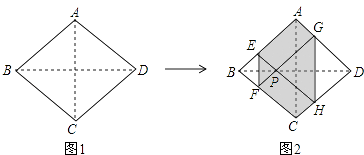
查看答案和解析>>【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是正方形ABCD的中心;
②当x= 时,EF+GH>AC;
时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是(写出所有正确判断的序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

相关试题

