【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣![]() 与 是关于1的平衡数;
与 是关于1的平衡数;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判断m+
,判断m+![]() 与5﹣
与5﹣![]() 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
参考答案:
【答案】(1)﹣1,﹣3+![]() ;(2)不是,理由见解析.
;(2)不是,理由见解析.
【解析】试题分析:(1)根据所给的例子,可得出平衡数的求法,由此可得出答案.
(2)根据所给的等式,解出m的值,进而再代入判断即可.
试题解析:(1)由题意得,3+(﹣1)=2,5﹣![]() +(﹣3+
+(﹣3+![]() )=2,
)=2,
∴3与﹣1是关于1的平衡数,5﹣![]() 与﹣3+
与﹣3+![]() 是关于1的平衡数;
是关于1的平衡数;
(2)不是.
∵(m+![]() )×(1﹣
)×(1﹣![]() )
)
=m﹣![]() m+
m+![]() ﹣3,
﹣3,
又∵(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,
,
∴m﹣![]() m+
m+![]() ﹣3=﹣5+3
﹣3=﹣5+3![]() ,
,
∴m﹣![]() m=﹣2+2
m=﹣2+2![]() .
.
即 m(1﹣![]() )=﹣2(1﹣
)=﹣2(1﹣![]() ).
).
∴m=﹣2.
∴(m+![]() )+(5﹣
)+(5﹣![]() )=(﹣2+
)=(﹣2+![]() )+(5﹣
)+(5﹣![]() )=3,
)=3,
∴(﹣2+![]() )与(5﹣
)与(5﹣![]() )不是关于1的平衡数.
)不是关于1的平衡数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知平面内一点
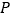 与一直线
与一直线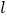 ,如果过点
,如果过点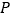 作直线
作直线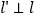 ,垂足为
,垂足为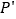 ,那么垂足
,那么垂足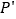 叫做点
叫做点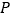 在直线
在直线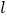 上的射影;如果线段
上的射影;如果线段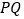 的两个端点
的两个端点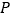 和
和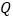 在直线
在直线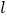 上的射影分别为点
上的射影分别为点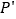 和
和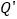 ,那么线段
,那么线段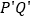 叫做线段
叫做线段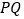 在直线
在直线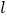 上的射影.
上的射影.如图①,已知平面内一点
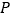 与一直线
与一直线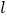 ,如果过点
,如果过点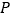 作直线
作直线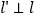 ,垂足为
,垂足为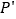 ,那么垂足
,那么垂足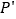 叫做点
叫做点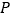 在直线
在直线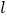 上的射影;如果线段
上的射影;如果线段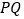 的两个端点
的两个端点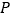 和
和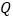 在直线
在直线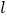 上的射影分别为点
上的射影分别为点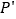 和
和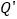 ,那么线段
,那么线段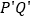 叫做线段
叫做线段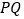 在直线
在直线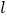 上的射影.
上的射影.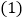 如图②,
如图②,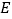 、
、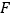 为线段
为线段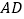 外两点,
外两点,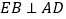 ,
,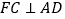 ,垂足分别为
,垂足分别为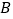 、
、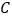 .
.则
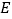 点在
点在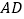 上的射影是________点,
上的射影是________点,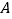 点在
点在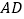 上的射影是________点,
上的射影是________点,线段
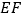 在
在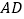 上的射影是________,线段
上的射影是________,线段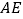 在
在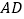 上的射影是________;
上的射影是________;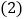 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)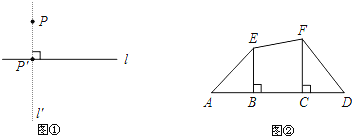
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
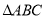 中,
中,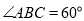 ,点
,点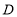 ,
,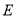 分别为
分别为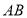 ,
,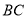 上一点,
上一点,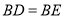 ,连接
,连接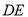 ,
,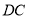 ,
,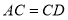 .
.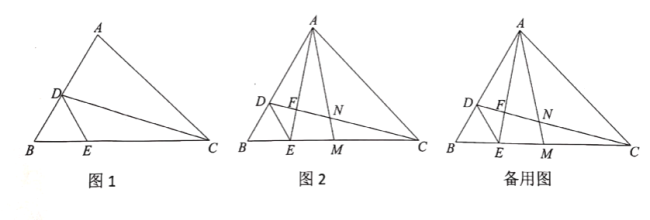
(1)如图1,若
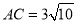 ,
,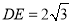 ,求
,求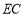 的长;
的长;(2)如图2,连接
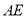 交
交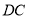 于点
于点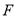 ,点
,点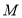 为
为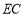 上一点,连接
上一点,连接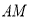 交
交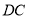 于点
于点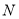 ,若
,若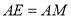 ,求证:
,求证: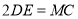 ;
;(3)在(2)的条件下,若
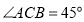 ,直接写出线段
,直接写出线段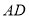 ,
,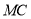 ,
,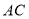 的等量关系.
的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=15,AC=20,BC边上的高AD=12,则BC的长为( )
A.25B.7C.25或7D.14或4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=
 ,BC=6cm,AC=10cm。
,BC=6cm,AC=10cm。(1)求AB的长;
(2)若P点从点B出发,以2cm/s的速度在BC所在的直线
 上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。
上运动,设运动时间为t秒,那么当t为何值时,△ACP为等腰三角形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小儿是同班同学,被分到了同一个学习小组,在一次数学活动课上,他们各自用一张面积为
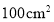 的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
的正方形纸片制作了一副七巧板,合作完成了如图所示的作品.请计算图中打圈部分的面积是( )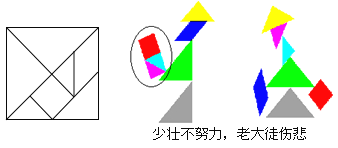
少壮不努力,老大徒伤悲
A.
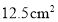 B.
B.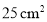 C.
C.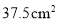 D.
D.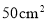
相关试题

