Question

【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

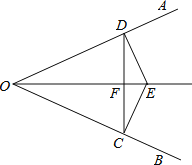
(1)求证：OE是CD的垂直平分线.

(2)若∠AOB=60°，请你探究OE，EF之间有什么数量关系?并证明你的结论.

Answer 1

【答案】(1)证明见解析；(2) OE=4EF.

【解析】试题分析：（1）先证△ODE≌△OCE，得出△DOC是等腰三角形，再根据等腰三角形三线合一得出OE是CD的垂直平分线；（2）分别求出∠AOE=30°，∠EDF=30°，根据直角三角形中，30°所对的直角边等于斜边的一半求解.

解：(1)∵E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，

∴DE=CE，又∵OE=OE，

∴Rt△ODE≌Rt△OCE，

∴OD=OC，

∴△DOC是等腰三角形，

又∵OE是∠AOB的平分线，

∴OE是CD的垂直平分线；

(2)∵OE是∠AOB的平分线,∠AOB=60°，

∴∠AOE=∠BOE=30°，

∵ED⊥OA，CD⊥OE，

∴OE=2DE,∠ODF=∠OED=60°，

∴∠EDF=30°，

∴DE=2EF，

∴OE=4EF.