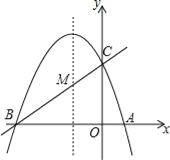
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
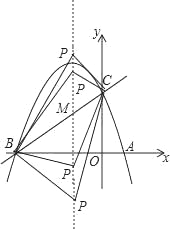
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)P的坐标为(-1,-2)或(-1,4) 或(-1,
;(2)M(-1,2);(3)P的坐标为(-1,-2)或(-1,4) 或(-1,![]() ) 或(-1,
) 或(-1,![]() ).
).
【解析】试题分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
试题解析:(1)依题意得: 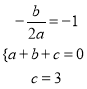 ,
,
解之得: 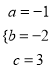
∴抛物线解析式为y=-x2-2x+3
∵对称轴为x=-1,且抛物线经过A(1,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2
即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2
即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2
即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1, ![]() ) 或(-1,
) 或(-1, ![]() ).
).
-
科目: 来源: 题型:
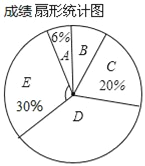
查看答案和解析>>【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别
成绩(分)
频数
A
50≤x<60
6
B
60≤x<70
m
C
70≤x<80
20
D
80≤x<90
36
E
90≤x<100
n
(1)频数分布表中的m= ,n= ;
(2)样本中位数所在成绩的级别是 ,扇形统计图中,E组所对应的扇形圆心角的度数是 ;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程kx2+2x﹣1=0有两个实数根,则k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(2a2)4=8a6
B.a3+a=a4
C.(a﹣b)2=a2﹣b2
D.a2÷a=a -
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,﹣2,0,1四个数中最小的数是( )
A.﹣1
B.-2
C.0
D.-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,①若a>0,b>0,则a+b>0;②同位角相等;③有两边和一个角分别对应相等的两个三角形全等;④三角形的最大角不小于60°;真命题有( )个
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-2,3)所在象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

