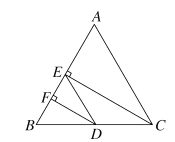
【题目】如图,在三角形ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.
参考答案:
【答案】∠EDF=∠BDF
【解析】试题分析:先根据平行线的性质得出∠ACE=∠DEC,再运用垂直于同一条直线的两直线平行得出DF∥CE,进而利用平行线的性质得出∠BDF=∠BCE,∠FDE=∠DEC,然后利用角平分线等量代换即可得出两角的关系.
试题解析:
解:∠EDF=∠BDF.
理由如下:∵AC∥ED,∴∠ACE=∠DEC.
∵CE⊥AB,DF⊥AB,∴∠AEC=∠AFD=90°,
∴DF∥CE,∴∠BDF=∠BCE,∠FDE=∠DEC,
∴∠FDE=∠ACE.
∵CE平分∠ACB,∴∠ECB=∠ACE.
∴∠EDF=∠BDF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查.在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示.
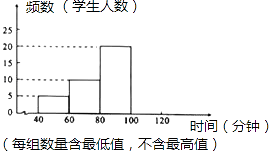
(1)这次被抽查的学生有人;
(2)请补全频数分布直方图;
(3)被调查这些学生每天完成课外作业时间的中位数在组(填时间范围);
(4)若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式乘法算式中,可以用平方差公式计算的是( )
A. (m-n)(n-m) B. (a+b)(-a-b)
C. (-a-b)(a-b) D. (a+b)(a+b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,以AB为直径作⊙O交于BC于D,DE⊥AC于E.
求证:DE是⊙O的切线.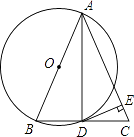
-
科目: 来源: 题型:
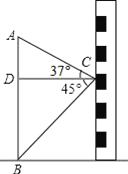
查看答案和解析>>【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
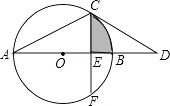
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF= ,求图中阴影部分的面积.
,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是真命题的是( )
A. 过直线外一点可以画无数条直线与已知直线平行
B. 如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°
C. 3条直线交于一点,对顶角最多有6对
D. 与同一条直线相交的两条直线相交
相关试题

