【题目】如图所示,在△ABC中,AB=AC,以AB为直径作⊙O交于BC于D,DE⊥AC于E.
求证:DE是⊙O的切线.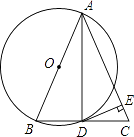
参考答案:
【答案】证明:连接OD,∵以AB为直径作⊙O交于BC于D,
∴∠ADB=90°,
∵AB=AC,
∴BD=DC,
∵AO=BO,
∴DO是△ABC的中位线,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线.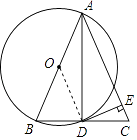
【解析】直接利用圆周角定理进而得出∠ADB=90°,再利用等腰三角形的性质结合三角形中位线定理得出OD⊥DE,即可得出答案.
【考点精析】本题主要考查了等腰三角形的性质和切线的判定定理的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣40(填“>”、“<”或“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查.在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示.
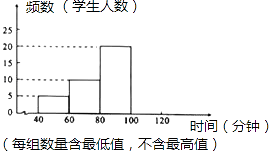
(1)这次被抽查的学生有人;
(2)请补全频数分布直方图;
(3)被调查这些学生每天完成课外作业时间的中位数在组(填时间范围);
(4)若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式乘法算式中,可以用平方差公式计算的是( )
A. (m-n)(n-m) B. (a+b)(-a-b)
C. (-a-b)(a-b) D. (a+b)(a+b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,CE⊥AB于E,DF⊥AB于F,AC∥ED,CE是∠ACB的平分线,试比较∠EDF与∠BDF的大小,并说明理由.
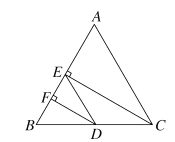
-
科目: 来源: 题型:
查看答案和解析>>【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
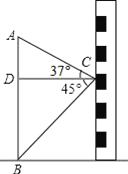
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
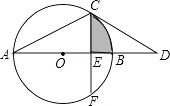
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF= ,求图中阴影部分的面积.
,求图中阴影部分的面积.
相关试题

