搜索
【题目】如图，点M、N分别是正方形ABCD的边CD、CB上的动点，满足DM=CN，AM与DN相交于点E，连接CE，若正方形的边长为2，则线段CE的最小值是______________．
参考答案：
【答案】
-1
【解析】
根据题意可得△DCN≌△ADM，可得∠CDN＝∠DAM，可证∠DEA＝90°，则点E是以AD为直径的圆上一点，则可得不等式，可解得线段CE的最小值．
取AD中点O，连接OE，OC
∵ABCD是正方形
∴AD＝CD，∠ADC＝∠DCB＝90°且DM＝CN
∴△ADM≌△DCN
∴∠CDN＝∠DAM
∵∠CDN＋∠ADN＝90°
∴∠DAM＋∠ADN＝90°
∴∠AED＝90°
∴点E是以AD为直径的圆上一点，
如图所示
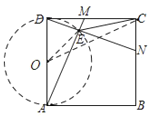
∵正方形ABCD的边长为2，O是AD中点
∴CD＝2，OD＝1＝OE
∴OC＝
=
∵EC≥OCOE＝1
∴EC的最小值为1
故答案为1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图①，在等边△ABC中，点M是BC边上的任意一点（不含端点B，C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ACN=∠ABC．
【类比探究】
（2）如图②，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ACN=∠ABC还成立吗？请说明理由．
【拓展延伸】
（3）如图③，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题
（1）如图①，点C是∠AOB边OB上的一点，在图中作出点C到OA的垂线段CD，垂足为D．再过C点作OA的平行线CE．
（2）如图②，在正方形网格中，每个小正方形的边长为1，△ABC的顶点都在正方形顶点上，将△ABC先向左平移2个单位，再向下平移3个单位，得到△A′B′C′，请你画出平移后的△A′B′C′．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，□ OABC的边OC落在x轴的正半轴上，点C(4，0)，B(6，2)，直线y=2x+1以每秒2个单位的速度向下平移，经过________秒该直线可将□OABC的面积平分．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度．为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了 名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )
A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目： 来源： 题型：
查看答案和解析>>【题目】王老师将3个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组部分统计数据．
摸球的次数
100
150
200
500
800
1000
摸到黑球的次数
23
31
60
127
203
251
摸到黑球的频率
0.23
0.21
0.30
0.254
0.253
___
___（1）根据上表数据计算
= ．估计从袋中摸出一个球是黑球的概率是 ．（精确到0. 01）（2）估算袋中白球的个数．
相关试题
