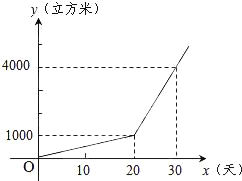
【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
参考答案:
【答案】(1)1000;(2)y=300x﹣5000;(3)40
【解析】试题分析:根据题意得出第20天的总用水量;y与x的函数关系式为分段函数,则需要分两段分别求出函数解析式;将y=7000代入函数解析式求出x的值.
试题解析:(1)第20天的总用水量为1000米3
当0<x<20时,设y=mx ∵函数图象经过点(20,1000),(30,4000) ∴m=50
y与x之间的函数关系式为:y=50x
当x≥20时,设y=kx+b ∵函数图象经过点(20,1000),(30,4000)
∴![]() 解得
解得![]() ∴y与x之间的函数关系式为:y=300x﹣5000
∴y与x之间的函数关系式为:y=300x﹣5000
(3)当y=7000时, 有7000=300x﹣5000,解得x=40
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,图像与y轴交点在x轴上方?
(3) 若一次函数y=(1-3k)x+2k-1经过点(3,4).请求出一次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量
折扣
邮费
汇费
不超过10本
九折
6元
每100元汇款需汇费1元
(汇款不足100元时按100元汇款收汇费)
超过10本
八折
总书价的10%
每100元汇款需汇费1元
(汇款不足100元的部分不收汇费)
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年李明家买了一辆轿车,他连续记录了一周中每天行驶的路程(如下表),以50km为标准,多于50km的记“+”,不足50km的记“-”,刚好506m的记“0”.
周一
周二
周三
周四
周五
周六
周日
路程(km)
-6
0
-12
7
-9
+15
+12
(1)请你求出李明家轿车一周中平均每天行驶多少千米?
(2)如果每行驶100km需要汽油8升,汽油价格6.85元/升,请计算李明家轿车一个月(按30天计算)的汽油费是多少元(精确到个位)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列计算过程,发现规律,利用规律猜想并计算:
1+2=
 =3;1+2+3=
=3;1+2+3= =6,1+2+3+4=
=6,1+2+3+4= =10;1+2+3+4+5=
=10;1+2+3+4+5= =15;…
=15;…(1)猜想:1+2+3+4+…+n= .
(2)利用上述规律计算:1+2+3+4+…+200;
(3)尝试计算:3+6+9+12+…3n的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB内部有三条射线,OE平分∠AOD,OC平分∠BOD.
(1)若∠AOB=90°,求∠EOC的度数;
(2)若∠AOB=α,求∠EOC的度数;
(3)如果将题中“平分”的条件改为∠EOA=
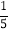 ∠AOD,∠DOC=
∠AOD,∠DOC= ∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
∠DOB,∠AOD=50°,且∠AOB=90°,求∠EOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
相关试题

