【题目】为满足同学们课外阅读的需求,某中学图书馆向出版社邮购科普系列图书,每本书单价为16元,书的价钱和邮费是通过邮局汇款,相关的书价折扣、邮费和汇款的汇费如下表所示(总费用=总书价+总邮费+总汇费)
购书数量 | 折扣 | 邮费 | 汇费 |
不超过10本 | 九折 | 6元 | 每100元汇款需汇费1元 (汇款不足100元时按100元汇款收汇费) |
超过10本 | 八折 | 总书价的10% | 每100元汇款需汇费1元 (汇款不足100元的部分不收汇费) |
(1)若一次邮购7本,共需总费用为 元.
(2)已知学校图书馆需购图书的总数是10的整倍数,且超过10本.
①若分次邮购,分别汇款,每次邮购10本,总费用为1064元时,共邮购了多本图书?
②若你是学校图书馆负责人,从节约的角度出发,在“每次邮购10本“与“一次性邮购”这两种方式中选择一种,你会选择哪一种?计算并说明理由.
参考答案:
【答案】(1)108.8元;(2)①共邮购了70本;②从节约的角度出发,选择一次性邮购的方式,理由见解析.
【解析】
(1)根据总费用=7本书的总价×0.9+总邮费+总汇费就可以求出结论;
(2)①设一共邮购了x本书,分![]() 邮购,需要书款为
邮购,需要书款为![]() 元,邮费为
元,邮费为![]()
元,汇费为![]() 元,根据题意建立方程求出其解就可以了;
元,根据题意建立方程求出其解就可以了;
②分别计算出每次邮购10本和一次邮购的总费用的表达式,再比较其大小就可以得出结论;
(1)由题意可得,
总书价为:16×7×0.9=100.8(元),
∴总的费用为:100.8+6+2=108.8(元),
故答案为:108.8元;
(2)①设共邮购了x本图书,
16×10×0.9=144(元),
∴![]()
解得,x=70,
答:共邮购了70本;
②从节约的角度出发,选择一次性邮购的方式,
理由:设共购买了x本,
按每次邮购10本,最后的总费用为:![]() (元),
(元),
一次性邮购的总书价和邮费为:16×0.8x(1+10%)=14.08x,
∵超过10本,不足100元的部分不收汇费,
∴汇费不大于:0.1408x元,
∵15.2x﹣(14.08x+0.1408x)=0.9792x>0,
∴从节约的角度出发,选择一次性邮购的方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表给出了某班6名同学的身高情况(单位:cm).
学生
A
B
C
D
E
F
身高(单位:cm)
165
____
166
____
____
172
身高与班级平
均身高的差值)
-1
+2
____
-3
+4
____
(1)完成表中空的部分;
(2)他们6人中最高身高比最矮身高高多少?
(3)如果身高达到或超过平均身高时叫达标身高,那么这6名同学身高的达标率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年十一黄金周期间,九寨沟7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
日期
1日
2日
3日
4日
5日
6日
7日
人数变化/万人
+0.5
+0.7
+0.8

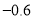
+0.2

(1)、请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?(5分)
(2)、如果9月30日旅游人数为2.5万人,平均每人消费500元,请问风景区在此7天内总收入为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠DAB=∠CAE,要使△ABC∽△ADE,则补充的一个条件可以是(注:只需写出一个正确答案即可).
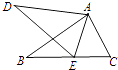
-
科目: 来源: 题型:
查看答案和解析>>【题目】水资源透支现象令人担忧,节约用水迫在眉睫,针对居民用水浪费现象,保定市政府和环保组织进行了调查,并制定出相应的措施.
(1)据环保组织调查统计,全市至少有6×106个水龙头、2×104个抽水马桶漏水,若一万个漏水的水龙头一个月能漏掉a立方米水;一万个漏水的马桶一个月漏掉b立方米水,则全市一个月仅这两项所造成的水流失量是多少?
(2)针对居民用水浪费现象,市政府将制定居民用水标准:规定每个三口之家每月的标准用水量,超过标准部分加价收费,不超标部分的水价为每立方米3.5元;超标部分为每立方米4.2元.若某家庭某月用水12立方米,交水费44.8元,请你通过列方程求出我市规定的三口之家每月的标准用水量为多少立方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律
在数轴上,把表示数1的点称为基准点,记作点O.对于两个不同点M和N,若点M和点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图1中MO=NO=2,则点M和点N互为基准变换点.
发现:(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
①若a=0,则b= ;若a=4,则b= ;
②用含a的式子表示b,则b= ;
应用:(2)对点A进行如下操作:先把点A表示的数乘以
 ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B.若点A与点B互为基准变换,则点A表示的数是多少?探究:(3)点P是数轴上任意一点,对应的数为m,对P点做如下操作:P点沿数轴向右移动k(k>0)个单位长度得到P1,P2为P1的基准变换点,点P2沿数轴向右移动k个单位长度得到点P3,点P4为P3的基准变换点,“…依次顺序不断的重复,得到P6…,求出数轴上点P2018表示的数是多少?(用含m的代数式表示)

相关试题

