【题目】如图,已知点![]() 、
、![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() .现在有一动点
.现在有一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向右运动,同时另一动点
个单位长度的速度向右运动,同时另一动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向左运动.
个单位长度的速度向左运动.
![]()
(1)与![]() 、
、![]() 两点相等的点
两点相等的点![]() 所对应的数是_________.
所对应的数是_________.
(2)两动点![]() 、
、![]() 相遇时所用时间为________秒;此时两动点所对应的数是_________.
相遇时所用时间为________秒;此时两动点所对应的数是_________.
(3)动点![]() 所对应的数是
所对应的数是![]() 时,此时动点
时,此时动点![]() 所对应的数是_________.
所对应的数是_________.
(4)当动点![]() 运动
运动![]() 秒钟时,动点
秒钟时,动点![]() 与动点
与动点![]() 之的距离是________单位长度.
之的距离是________单位长度.
(5)经过________秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.
参考答案:
【答案】30; 20; 40; 52; 25; 12或28.
【解析】
(1)根据数轴上A、B两点所表示的数为a、b,则AB的中点所表示的数可以用公式![]() 计算;
计算;
(2)设两动点相遇时间为t秒,P、Q两点运动的路程之和为总路程,列方程求解即可;用80-2t即可求得此时两动点对应的数;
(3)先求出动点P对应的点是22时运动的时间,再根据Q和P运动时间相等计算Q点运动路程,进而求得点Q对应的数;
(4)根据题意P、Q两点25秒运动的路程和减去总路程就是PQ两点间的距离;
(5)根据题意,分两种情况进行解答,即:①相遇前相距40个单位长度,②相遇后相距40个单位长度,分别列方程求解即可.
解:(1)AB的中点C所对应的数为:![]()
(2)设两动点相遇时间为t秒,(2+3)t=80-(-20) 解得:t=20(秒)
80-2t=80-2×20=40,或-20+3×20=40
∴此时两动点所对应的点为40;
(3)22-(-20)=42, 80-42÷3×2=52
∴动点![]() 所对应的数是
所对应的数是![]() 时,此时Q所对应的数为52;
时,此时Q所对应的数为52;
(4)∵20秒相遇,∴(2+3) ×25-[80-(-20)]=25
(5)P、Q两点相距40个单位长度,分两种情况
AB=80-(-20)=100
①相遇前,(100-40) ÷(3+2)=60÷5=12(秒)
②相遇后,(100+40)÷(2+3)=140÷5 =28(秒)
∴经过12或28秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮
第2轮
第3轮
第4轮
第5轮
第6轮
甲
10
14
12
18
16
20
乙
12
11
9
14
22
16
下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分)
60
70
80
90
100
人数(人)
1
5
x
y
2
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D,E,F分别为BC,AD,AE的中点,且S△ABC=4cm2,则阴影部分面积S=( )cm2.
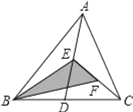
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
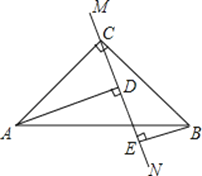
查看答案和解析>>【题目】已知:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.求证:①△ADC≌△CEB;②DE=AD﹣BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列各组条件中,不能说明
 的是( )
的是( )A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
相关试题

