【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
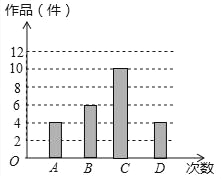
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
参考答案:
【答案】(1)抽样调查;(2)全校共征集作品180件; (3)恰好抽中一男一女的概率为![]() .
.
【解析】
试题分析:(1)杨老师从全校30个班中随机抽取了4个班,属于抽样调查.(2)由题意得:所调查的4个班征集到的作品数为:6÷![]() =24(件),C班作品的件数为:24﹣4﹣6﹣4=10(件);继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
=24(件),C班作品的件数为:24﹣4﹣6﹣4=10(件);继而可补全条形统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽中一男一女的情况,再利用概率公式即可求得答案.
试题解析:(1)杨老师从全校30个班中随机抽取了4个班,属于抽样调查.故答案为抽样调查.
(2)所调查的4个班征集到的作品数为:6÷![]() =24件,平均每个班
=24件,平均每个班![]() =6件,C班有10件,
=6件,C班有10件,
∴估计全校共征集作品6×30=180件.
条形图如图所示,
(3)画树状图得:
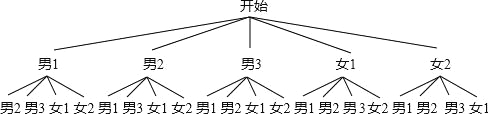
∵共有20种等可能的结果,两名学生性别相同的有8种情况,
∴恰好抽中一男一女的概率为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】类比学习:一动点沿着数轴先向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)=1.若坐标平面上的点有如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫做这一平移的“平移量”,“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2},{1,2}+{3,1}.
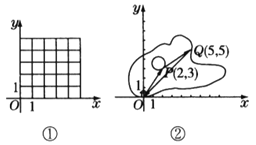
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B;若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC.
(3)如图②所示,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】24表示( )
A.2×2×2×2B.2×4 C.4×4 D.2+2+2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,左右两幅图案关于y轴对称,右边图案中的左、右两朵花花心的坐标分别是(2,5)和(3,4).
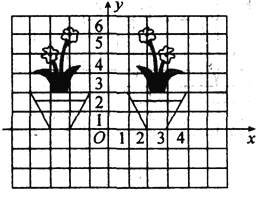
(1)试确定左边图案中的左、右两朵花花心的坐标.
(2)如果将右边图案沿x轴向右平移2个单位长度,那么它的左、右两朵花的花心坐标将发生什么变化?
(3)如果将右边图案中的所有点的横坐标保持不变,纵坐标都加1,那么图案将发生什么变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2x3(﹣x2)的结果是( )
A.﹣2x5
B.2x5
C.﹣2x6
D.2x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣3x=0的解是_____.
相关试题

