【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级美联点”为Q(3![]() +4,1+3
+4,1+3![]() ),即Q(7,13).
),即Q(7,13).
(1)已知点A(一2,6)的“![]() 级关联点”是点
级关联点”是点![]() ,求点
,求点![]() 的坐标。
的坐标。
(2)已知点M(m一1,2m)的“一3级关联点”M’位于y轴上.求点M’的坐标。
参考答案:
【答案】(1) ![]() (5,1); (2)
(5,1); (2)![]() (0,-16).
(0,-16).
【解析】
(1)根据关联点的定义,结合点的坐标即可得出结论.
(2)根据关联点的定义和点M(m-1,2m)的“-3级关联点”M′位于y轴上,即可求出M′的坐标.
解(1)因为点A(-2,6)的“![]() 级关联点”是点
级关联点”是点![]() ,所以∴A1(-2×
,所以∴A1(-2×![]() +6,-2+
+6,-2+![]() ×6),即
×6),即![]() 为
为![]() (5,1);
(5,1);
(2)因为点M(m- 1,2m)的“一3级关联点”为M’(-3m(m-1)+2m·m-1+(-3)·2m).又因为点M’位于y轴上,所以-3(m-1)+2m=0, 解得m=3. 所以m-1+(-3)·2m=-16,
所以M’(0,-16)
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定两数a,b之间的一种运算,记作(a,b):如果
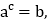
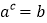 ,那么(a,b)=c.
,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,
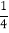
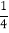 )=_______.
)=_______.(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分两次在同一粮店内买粮食,两次的单价不同,甲每次购粮100千克,乙每次购粮100元.若规定:谁两次购粮的平均单价低,谁的购粮方式就合算.那么这两次购粮( )
A. 甲合算 B. 乙合算
C. 甲、乙一样 D. 要看两次的价格情况
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( )
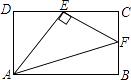
A.△ADE∽△ECF
B.△BCF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解答下列各题:
(1)化简:
 ;
;(2)解分式方程:
 ;
;(3)已知关于x的方程
 有一个正数解,求m的取值范围.
有一个正数解,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC与△A'B'C'在平面直角坐标系中的位置如图所示
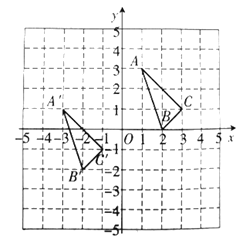
(1)分别写出下列各点的坐标:A_______ B_______ C_______
(2)△ABC由△A'B'C'经过怎样的平移得到?
(3)若点P(x,y)是△ABC内部点,则A'B'C' 内部的对应点P'的坐标为
(4)求△ABC的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个)

相关试题

