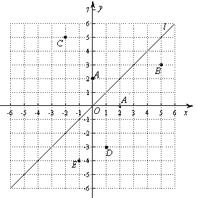
【题目】如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′_______、C′_______;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为________;
运用与拓展:
(3)图中在直线l上取一点Q,使Q到D(1,-3),E(-1,-4)两点的距离之和最小,则点Q的坐标是____________。
参考答案:
【答案】(1)![]() ;(2)(b,a);(3)(
;(2)(b,a);(3)(![]() )
)
【解析】
(1)易找到点![]() 关于第一、三象限角平分线的对称点
关于第一、三象限角平分线的对称点![]() 的坐标为
的坐标为![]() ,再结合已知的点
,再结合已知的点![]() 的坐标,我们不难猜想点C′坐标是
的坐标,我们不难猜想点C′坐标是![]() ;
;
(2)可以发现![]() 被第一、三象限角平分线垂直且平分,由此可以推想到坐标平面内任一点
被第一、三象限角平分线垂直且平分,由此可以推想到坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为(
的坐标为(![]() ,即它们纵、横坐标互换位置;
,即它们纵、横坐标互换位置;
(3)由(2)得,D(1,﹣3)关于直线![]() 的对称点
的对称点![]() 的坐标为(﹣3,1),连接
的坐标为(﹣3,1),连接![]() 交直线
交直线![]() 于点
于点![]() ,此时点
,此时点![]() 到
到![]() 两点的距离之和最小.
两点的距离之和最小.
(1)如图:通过观察知![]() ;
;
(2)由(1) 可以推想到坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为(
的坐标为(![]() ,即它们纵、横坐标互换位置;
,即它们纵、横坐标互换位置;
答案是:(b,a);
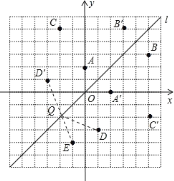
(3)由(2)得,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为(-3,1),连接
的坐标为(-3,1),连接![]() 交直线
交直线![]() 于点
于点![]() ,此时点
,此时点![]() 到
到![]() 两点的距离之和最小.
两点的距离之和最小.
设过D′(-3,1)、E(-1,-4)直线的解析式为![]() ,
,
则![]()
∴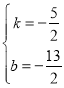
∴直线D′E的解析式为:![]()
由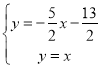
得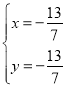
∴所求Q点的坐标为(![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有( )①图1中的BC长是8cm,②图2中的M点表示第4秒时y的值为24cm2,③图1中的CD长是4cm,④图2中的N点表示第12秒时y的值为18cm2,⑤图1的总面积为72 cm2

A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(-2,-3),B(1,0),C(3,4),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图
 ,已知
,已知 是⊙
是⊙ 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点 ,使
,使 为“智慧三角形”(画出点
为“智慧三角形”(画出点 的位置,保留作图痕迹);
的位置,保留作图痕迹);⑵如图
 ,在正方形
,在正方形 中,
中, 是
是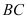 的中点,
的中点, 是
是 上一点,且
上一点,且 ,试判断
,试判断 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;运用:
⑶如图
 ,在平面直角坐标系
,在平面直角坐标系 中,⊙
中,⊙ 的半径为
的半径为 ,点
,点 是直线
是直线 上的一点,若在⊙
上的一点,若在⊙ 上存在一点
上存在一点 ,使得
,使得 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间
(小时)
2
2.5
3
3.5
4
学生人数(名)
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图


请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,

 ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为  ;
; (2)请你补全条形统计图;
(3)若该校有
 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
相关试题

