【题目】如图,反比例函数y= ![]() (k≠0,x>0)的图像与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图像于点D,且AB=3BD.
(k≠0,x>0)的图像与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图像于点D,且AB=3BD. 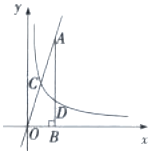
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
参考答案:
【答案】
(1)解:∵A(1,3),
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1
(2)解:由(1)知,k=1,
∴反比例函数的解析式为;y= ![]() ,
,
解: 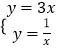 ,
,
解得: 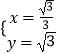 或
或 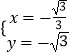 ,
,
∵x>0,
∴C( ![]() ,
, ![]() )
)
(3)解:如图,作C关于y轴的对称点C′,连接C′D交y轴于M,
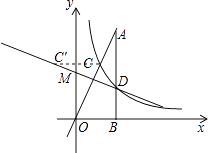
则d=MC+MD最小,
∴C′(﹣ ![]() ,
, ![]() ),
),
设直线C′D的解析式为:y=kx+b,
∴ 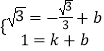 ,∴
,∴ ![]() ,
,
∴y=(3﹣2 ![]() )x+2
)x+2 ![]() ﹣2,
﹣2,
当x=0时,y=2 ![]() ﹣2,
﹣2,
∴M(0,2 ![]() ﹣2).
﹣2).
【解析】(1)根据A坐标,以及AB=3BD求出D坐标,代入反比例解析式求出k的值;(2)直线y=3x与反比例解析式联立方程组即可求出点C坐标;(3)作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,得到C′(﹣ ![]() ,
, ![]() ),求得直线C′D的解析式为y=﹣
),求得直线C′D的解析式为y=﹣ ![]() x+1+
x+1+ ![]() ,直线与y轴的交点即为所求.
,直线与y轴的交点即为所求.
【考点精析】解答此题的关键在于理解轴对称-最短路线问题的相关知识,掌握已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(3a2b﹣ab2)﹣(﹣3ab2+2a2b),其中a=﹣1,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形有两条边长分别为5和10,则这个等腰三角形的周长为( )
A. 15 B. 20 C. 25或20 D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.x3x2=2x6
B.x4x2=x8
C.(﹣x2)3=﹣x6
D.(x3)2=﹣x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】(7分)某地政府急灾民之所需,立即组织12辆汽车,将A、B、C三种救灾物资共92吨一次性运往灾区,甲、乙、丙三种车型的汽车分别运载A、B、C三种物资,每辆车按运载量满装物资。假设装运A、B品种物资的车辆数分别为
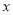 、
、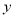 ,根据下表提供的信息解答下列问题:
,根据下表提供的信息解答下列问题:车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
(1)装运C品种物资车辆数为 辆(用含
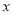 与
与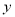 的代数式表示);
的代数式表示);(2)试求A、B、C三种物资各几吨。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为﹣1,那么与A点相距3个单位长度的点所对应的有理数为_____.
相关试题

