【题目】(8分)将一张长方形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°.
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.

参考答案:
【答案】(1)∠1=52°;(2)证明见解析.
【解析】
试题(1)图形的折叠中隐含着角和线段的相等,由题, 将一张矩形纸条ABCD按如图所示沿EF折叠,∠FEC=64o, ∠FEC′=64o,即∠BEC′=180o-∠FEC-∠FEC′= 52o,因为AD∥BC,所以∠1=∠AGC′=∠BEC′=52o;
(2)只要找到两个底角相等即可,因为∠FEC=64o,AD∥BC,所以∠GFE=∠FEC=64o,又因为∠FEC′=64o,所以GF=GE, 即△EFG是等腰三角形.
试题解析:(1)如图:∵∠FEC=64o,据题意可得:∠FEC′=64o,
∴∠BEC′=180o-∠FEC-∠FEC′= 52o,
又∵AD∥BC,
∴∠1="∠AGC′=" ∠BEC′=52o.
(2)证明:∵∠FEC=64o,AD∥BC,
∴∠GFE=∠FEC=64o,
又∵∠FEC′=64o,
∴∠FEG=∠GEF=64o,
∴GF=GE,即△EFG是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
 ,其中
,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为直径的圆交△ABC的两边AB、AC于点D、E,点E恰为AC的中点,BF为△ABC的外角平分线,点F在圆上,请你仅用一把无刻度的直尺,过点A作一条线段,将△ABC分成面积相等的两部分.
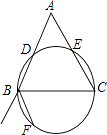
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为∠AOB内一定点,M,N分别是射线OA,OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=___________.
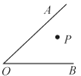
-
科目: 来源: 题型:
查看答案和解析>>【题目】有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
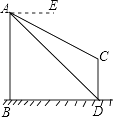
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
相关试题

