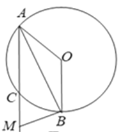
【题目】在圆![]() 中,
中,![]() 、
、![]() 是圆
是圆![]() 的半径,点
的半径,点![]() 在劣弧
在劣弧![]() 上,
上,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.

(1)如图1,试说明:![]() 平分
平分![]() ;
;
(2)如图2,点![]() 在弦
在弦![]() 的延长线上,连接
的延长线上,连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长;
的长;
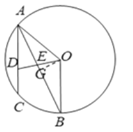
(3)如图3,点![]() 在弦
在弦![]() 上,与点
上,与点![]() 不重合,连接
不重合,连接![]() 与弦
与弦![]() 交于点
交于点![]() ,设点
,设点![]() 与点
与点![]() 的距离为
的距离为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]() 的长为4或8;(3)
的长为4或8;(3)![]() ,
, ![]() .
.
【解析】
(1)由AO=BO知∠OAB=∠B,根据OB∥AC知∠B=∠CAB,据此可得∠OAB=∠CAB,即可得证;
(2)①∠AMB=90°时,作OH⊥AC可得AH=HC=![]() AC=6,由勾股定理求得OH=BM=8,根据矩形OBMH知HM=OB=10,由CM=HM-HC可得答案;②∠ABM=90°时,由①可知AB=8
AC=6,由勾股定理求得OH=BM=8,根据矩形OBMH知HM=OB=10,由CM=HM-HC可得答案;②∠ABM=90°时,由①可知AB=8![]() 、cos∠CAB
、cos∠CAB![]() ,在Rt△ABM中根据cos∠CAB=
,在Rt△ABM中根据cos∠CAB=![]() 可得AM=20,继而得出答案;
可得AM=20,继而得出答案;
(3)作OG⊥AB,由(1)知sin∠OAG=sin∠CAB,从而sin∠CAB=![]() ,结合OA=10求得OG=2
,结合OA=10求得OG=2![]() ,根据AC∥OB知
,根据AC∥OB知 ![]() ,即
,即![]() ,据此求得BE=
,据此求得BE=![]() ,利用y=
,利用y=![]() ×BE×OG可得答案.
×BE×OG可得答案.
(1)证明:∵![]() 、
、![]() 是圆
是圆![]() 的半径,
的半径,
∴![]() ∴
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(2)解:由题意可知![]() 不是直角,
不是直角,
所以![]() 是直角三角形只有以下两种情况:
是直角三角形只有以下两种情况:
![]() 和
和![]() ,
,
①当![]() ,点
,点![]() 的位置如图,
的位置如图,

过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
∵![]() 经过圆心∴
经过圆心∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 是矩形,∴
是矩形,∴![]() ,
,
∴![]() ;
;
②当![]() ,点
,点![]() 的位置如图,
的位置如图,
由①可得![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
![]() ,
,
综上所述,![]() 的长为4或8.
的长为4或8.
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
由(1)、(2)可知,![]() ,
,
由(2)可得:![]() ,
,
∵![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ∴
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
自变量![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 经过正方形网格中的格点
经过正方形网格中的格点 、
、 、
、 、
、 ,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的
,请你仅用网格中的格点及无刻度的直尺分别在图1、图2、图3中画出一个满足下列两个条件的 :
: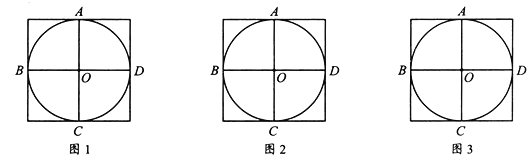
(1)顶点
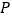 在
在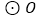 上且不与点
上且不与点 、
、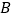 、
、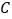 、
、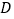 重合;
重合;(2)
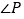 在图1、图2、图3中的正切值分别为1、
在图1、图2、图3中的正切值分别为1、 、2.
、2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
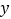 是
是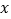 (
( )的函数,表1中给出了几组
)的函数,表1中给出了几组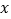 与
与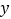 的对应值:
的对应值:表1:
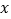
…

1

2

3
…
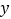
…
6
3
2

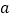
1
…
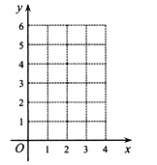
(1)以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出
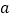 的值;
的值;(2)如果一次函数图像与(1)中图像交于
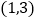 和
和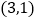 两点,在第一、四象限内当
两点,在第一、四象限内当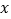 在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案.
在什么范围时,一次函数的值小于(1)中函数的值?请直接写出答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的2倍,则这个矩形是给定矩形的“加倍”矩形.如图,矩形
 是矩形
是矩形 的“加倍”矩形.
的“加倍”矩形.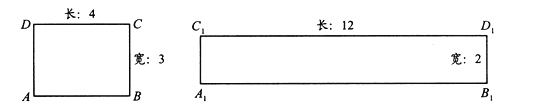
解决问题:
(1)当矩形的长和宽分别为3,2时,它是否存在“加倍”矩形?若存在,求出“加倍”矩形的长与宽,若不存在,请说明理由.
(2)边长为
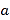 的正方形存在“加倍”正方形吗?请做出判断,并说明理由.
的正方形存在“加倍”正方形吗?请做出判断,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于点
轴交于点 ,交
,交 轴于点
轴于点 ,直线
,直线 过点
过点 与
与 轴交于点
轴交于点 ,与抛物线的另一个交点为
,与抛物线的另一个交点为 ,作
,作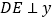 轴于点
轴于点 .设点
.设点 是直线
是直线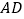 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点 、
、 重合),过点
重合),过点 作
作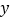 轴的平行线,交直线
轴的平行线,交直线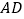 于点
于点 ,作
,作 于点
于点 .
.
(1)填空:
 __________,
__________, __________,
__________, __________;
__________;(2)探究:是否存在这样的点
 ,使四边形
,使四边形 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)设
 的周长为
的周长为 ,点
,点 的横坐标为
的横坐标为 ,求
,求 与
与 的函数关系式,并求出
的函数关系式,并求出 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,AD=2
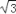 ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )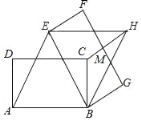
A.
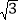 B. 2 C.
B. 2 C. 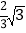 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】Windows2000下有一个有趣的“扫雷”游戏.如图是“扫雷”游戏的一部分,说明:图中数字2表示在以该数字为中心的周边8个方格中有2个地雷,小旗表示该方格已被探明有地雷.现在还剩下
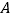 、
、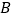 、
、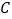 三个方格未被探明,其他地方为安全区(包括有数字的方格),则
三个方格未被探明,其他地方为安全区(包括有数字的方格),则 、
、 、
、 三个方格中有地雷概率最大的方格是( )
三个方格中有地雷概率最大的方格是( )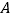
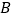
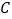
2
2
A. A B. B C. C D. 无法确定
相关试题

