【题目】在平面直角坐标系xOy中,直线l:y=x+b与x轴交于点A(﹣2,0),与y轴交于点B.双曲线y![]() 与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
与直线l交于P,Q两点,其中点P的纵坐标大于点Q的纵坐标
(1)求点B的坐标;
(2)当点P的横坐标为2时,求k的值;
(3)连接PO,记△POB的面积为S.若![]() ,结合函数图象,直接写出k的取值范围.
,结合函数图象,直接写出k的取值范围.
参考答案:
【答案】(1)点B的坐标为(0,2);(2)k的值为8;(3)![]() k<3.
k<3.
【解析】
(1)有点A的坐标,可求出直线的解析式,再由解析式求出B点坐标.
(2)把点P的横坐标代入直线解析式即可求得点P的纵坐标,然后把点P代入反比例函数解析式即可得k值.
(3)根据△POB的面积为S的取值范围求点P的横坐标取值,然后把横坐标代入直线解析式,即可求得点P纵坐标的取值范围,进而求得k的取值范围.
解:(1)∵直线l:y=x+b与x轴交于点A(﹣2,0)
∴﹣2+b=0
∴b=2
∴一次函数解析式为:y=x+2
∴直线l与y轴交于点B为(0,2)
∴点B的坐标为(0,2);
(2)∵双曲线y![]() 与直线l交于P,Q两点
与直线l交于P,Q两点
∴点P在直线l上
∴当点P的横坐标为2时,y=2+2=4
∴点P的坐标为(2,4)
∴k=2×4=8
∴k的值为8
(3)如图:
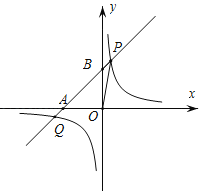
S△BOP![]() 2×xp=xp,
2×xp=xp,
∵![]() ,
,
∴![]() xp<1,
xp<1,
∴![]() yp<3,
yp<3,
∴![]() k<3
k<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆
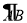 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1
位置2
位置3
位置4
位置5
位置6
位置…
AP
0.00
1.00
2.00
3.00
4.00
5.00
…
BC
6.00
5.48
4.90
4.24
3.46
2.45
…
OD
6.71
7.24
7.07
6.71
6.16
5.33
…
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
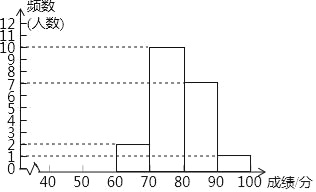
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数
方差
中位数
甲
79.6
36.84
78.5
乙
77
147.2
m
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年
2015年
2016年
2017年
2018年
出线成绩(百分制)
79
81
80
81
82
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
-
科目: 来源: 题型:
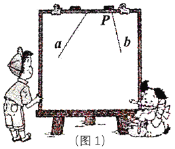
查看答案和解析>>【题目】已知:如图1,直线
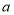 ,
,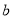 所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?
所成的角跑到画板外面去了,你有什么办法作出这两条直线所成角的角平分线?小明的做法是:
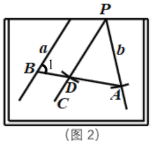
(1)如图2,画
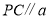 ;
;(2)以
 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线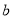 ,
,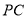 于点
于点 ,
,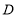 ;
;(3)连结
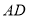 并延长交直线
并延长交直线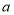 于点
于点 ;
;请你先完成下面的证明,然后完成第(4)步作图:
∵
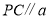
∴
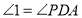 ( )
( )∵以
 为圆心,任意长为半径画圆弧,分别交直线
为圆心,任意长为半径画圆弧,分别交直线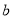 ,
,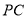 于点
于点 ,
,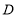
∴

∴
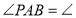
∴
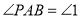
∴以直线
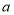 ,
,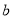 的交点和点
的交点和点 、
、 为顶点所构成的三角形为等腰三角形( )
为顶点所构成的三角形为等腰三角形( )根据上面的推理证明完成第(4)步作图
(4)请在图2画板内作出“直线
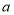 ,
,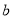 所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.
所成的跑到画板外面去的角”的平分线(画板内的部分),尺规作出图形,并保留作图痕迹.第(4)步这么作图的理论依据是: .
-
科目: 来源: 题型:
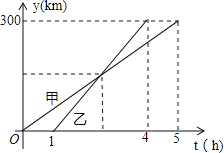
查看答案和解析>>【题目】甲、乙两车从
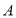 城出发匀速行驶至
城出发匀速行驶至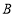 城.在整个行驶过程中,甲、乙两车离
城.在整个行驶过程中,甲、乙两车离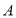 城的距离
城的距离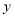 (千米)与甲车行驶的时间
(千米)与甲车行驶的时间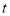 (小时)之间的函数关系如图所示.则下列结论:
(小时)之间的函数关系如图所示.则下列结论:①
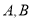 两城相距
两城相距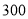 千米;
千米;②乙车比甲车晚出发
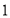 小时,却早到
小时,却早到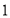 小时;
小时;③乙车出发后
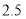 小时追上甲车;
小时追上甲车;④当甲、乙两车相距
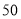 千米时,
千米时,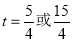
其中正确的结论有( )
A.
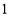 个B.
个B.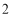 个C.
个C.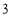 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a﹣b+c>0;②3a+b=0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.其中正确结论的是______________(只填序号)

相关试题

