【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
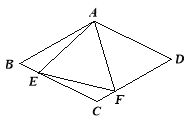
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
参考答案:
【答案】(1)证明过程见解析;(2)4+2![]()
【解析】
试题分析:(1)连接AC,根据菱形的性质以及∠BAD=120°得出∠BAE=∠FAC以及△ABC和△ACD为正三角形,从而得出△ABE和△ACF全等,从而得出答案;(2)根据三角形全等得出△ABE的面积=△ACF的面积,从而得出四边形AECF的面积=△ABC的面积,从而求出△ABC的面积得出四边形的面积,根据垂线段最短得出当正三角形AEF的边AE与BC垂直时,边AE最短,从而求出最小值.
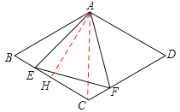
试题解析:(1)如图,连接AC∵四边形ABCD为菱形,∠BAD=120°,
∠BAE+∠EAC=60°,∠FAC+∠EAC=60°,∴∠BAE=∠FAC
∵∠BAD=120°,∴∠ABC=60°.∴△ABC和△ACD为等边三角形
∴∠ACF=60°,AC=AB ∴∠ABE=∠AFC ∴在△ABE和△ACF中,∵∠BAE=∠FAC,AB=AC,∠ABE=∠AFC,∴△ABE≌△ACF(ASA) ∴BE=CF
(2)四边形AECF的面积不变,△CEF的周长发生变化.理由如下:
由(1)得△ABE≌△ACF,则![]() .∴
.∴![]() ,是定值
,是定值
作AH⊥BC于H点,则BH=2,
![]() .
.
△CEF的周长=CE+CF+EF=CE+BE+EF=BC+EF=BC+AE
由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的周长会随着AE的变化而变化,且当AE最短时,△CEF的周长会最小=4+![]() ,
,

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的关联角.
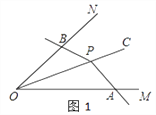
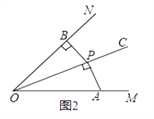
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
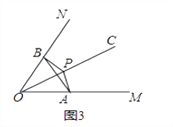
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
(3)如图4,点C是函数y=
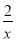 (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.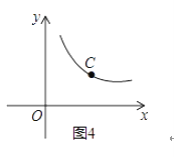
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 方程5x2=x有两个不相等的实数根
B. 方程x2﹣8=0有两个相等的实数根
C. 方程2x2﹣3x+2=0有两个整数根
D. 当k>
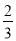 时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根
时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】高新一中新图书馆在“校园书香四溢”活动中迎来了借书高潮,上周借书记录如下表:(超过100册的部分记为正,少于100册的部分记为负)
(1)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(2)上星期平均每天借出多少册书?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=
 ∠BAE;
∠BAE;(2)求证:PG=PB;
(3)若AB=
 ,BC=3,求出BG的长.
,BC=3,求出BG的长. 
相关试题

