【题目】如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的关联角.
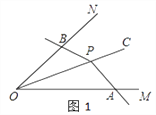
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
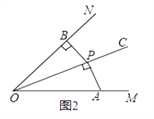
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
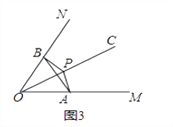
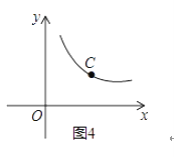
(3)如图4,点C是函数y=![]() (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
参考答案:
【答案】是
【解析】试题分析:(1)先判断出△OBP∽△OPA,即可;
(2)先根据关联角求出OA×OB=4,再利用三角形的面积公式,以及相似,得到∠OAP=∠OPB,即可;
(3)根据条件分情况讨论,点B在y轴正半轴和负半轴,在负半轴时,经过计算,不存在,②在正半轴时,由BC=2AC判断出点C是线段AB的一个三等分点,即可.
试题解析:(1)∵P为∠MON平分线OC上一点,
∴∠BOP=∠AOP,
∵PB⊥ON于B,AP⊥OC于P,
∴∠OBP=∠OPA,
∴△OBP∽△OPA,
∴![]() ,
,
∴OP2=OA×OB,
∴∠APB是∠MON的关联角.
故答案为是.
(2)①如图,过点A作AH⊥OB,
∵∠APB是∠MON的关联角,OP=2,
∴OA×OB=OP2=4,
在Rt△AOH中,∠AOH=90°,
∴sin∠AOH=![]() ,
,
∴AH=OAsin∠AOH,
∴S△AOB=![]() OB×AH=
OB×AH=![]() OB×OA×sin60°=
OB×OA×sin60°=![]() ×OP2×
×OP2×![]() =
=![]() ,
,
∵OP2=OA×OB,
∴![]() ,
,
∵点P为∠MON的平分线上一点,
∴∠AOP=∠BOP=![]() ∠MON=30°,
∠MON=30°,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°-30°=150°,
②由①有,S△AOB=![]() OB×OA×∠MON=
OB×OA×∠MON=![]() m2×sinα;
m2×sinα;
(3)∵过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,
∴只有点A在x轴正半轴,
①当点B在y轴负半轴时,点A只能在x轴正半轴.即:点P只能在第四象限,
设A(m,0),B(0,n)(m>0,n<0)
∴OA=m,OB=-n,
∵BC=2CA,
∴点A是BC中点,
∴点C(2m,-n),
∵点C在双曲线y=![]() 上,
上,
∴2m×(-n)=2,
∴mn=-1,
∵∠AOB的关联角∠APB
∴OP2=OA×OB=|m||n|=1span>,
∴OP=1,
∵点P在∠AOB的平分线上,设P(a,-a)(a>0),
∴OP2=2a2,
∴2a2=1,
∴a=![]() 或a=-
或a=-![]() (舍),
(舍),
∴点P(![]() ,-
,-![]() )
)
②当点B在y轴正半轴,由于BC=2CA,所以,点A只能在x轴正半轴上,
设A(m,0),B(0,n)(m>0,n>0)
∴点C(![]() ,
, ![]() ),
),
∴![]() ×
×![]() =2,
=2,
∴mn=9,
∵∠AOB的关联角∠APB
∴OP2=OA×0B=mn=9,
∴OP=3,
∵点P在∠AOB的平分线上,即:点P在第一象限,设P(a,a),(a>0)
∴OP2=2a2,
∴2a2=9,
∴a=![]() 或a=-
或a=-![]() (舍)
(舍)
即:点P(![]() ,
, ![]() ),
),
综上所述,点P的坐标为:(![]() ,-
,-![]() )或(
)或(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,
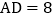 ,点E在边CD上,且
,点E在边CD上,且 ,
,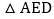 与
与 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形 以点A为中心,把
以点A为中心,把 顺时针旋转
顺时针旋转 ,得到
,得到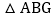 ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.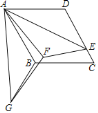
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条公路上顺次有
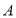 、
、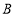 、
、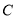 三地,甲、乙两车同时从
三地,甲、乙两车同时从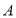 地出发,分别匀速前柱
地出发,分别匀速前柱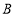 地、
地、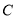 地,甲车到达
地,甲车到达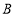 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达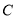 地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回
地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回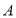 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程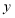 (千米)与时间
(千米)与时间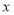 (时)(从两车出发时开始计时)之间的变化情况如图所示.
(时)(从两车出发时开始计时)之间的变化情况如图所示.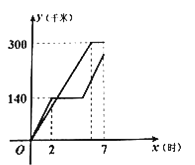
(1)在这个变化过程中,自变量是______,因变量是______.
(2)甲车到达
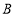 地停留的时长为______小时,乙车从出发到返回
地停留的时长为______小时,乙车从出发到返回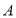 地共用了______小时.
地共用了______小时.(3)甲车的速度是______千米/时,乙车的速度是______千米/时.
(4)
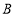 、
、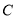 两地相距______千米,甲车返回
两地相距______千米,甲车返回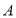 地途中
地途中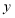 与
与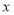 之间的关系式是______(不必写出自变量取值范围).
之间的关系式是______(不必写出自变量取值范围). -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,点
,点 在边
在边 上,点
上,点 在边
在边 上(点
上(点 、点
、点 不与所在线段端点重合),
不与所在线段端点重合), ,连接
,连接 ,
, .射线
.射线 ,延长
,延长 交射线
交射线 于点
于点 ,点
,点 在直线
在直线 上,且
上,且 .
.
(1)如图1所示,点
 在
在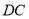 的延长线上,求
的延长线上,求 的度数.
的度数.(2)若
 ,其它条件不变,当点
,其它条件不变,当点 在
在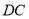 的延长线上时,
的延长线上时, ______;当点
______;当点 在
在 的延长线上时,
的延长线上时, ______.(用含
______.(用含 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 方程5x2=x有两个不相等的实数根
B. 方程x2﹣8=0有两个相等的实数根
C. 方程2x2﹣3x+2=0有两个整数根
D. 当k>
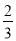 时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根
时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.
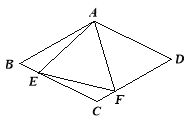
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
相关试题

