【题目】如图,∠MAN=60°,AP平分∠MAN,点B是射线AP上一定点,点C在直线AN上运动,连接BC,将∠ABC(0°<∠ABC<120°)的两边射线BC和BA分别绕点B顺时针旋转120°,旋转后角的两边分别与射线AM交于点D和点E.

(1)如图1,当点C在射线AN上时,
①请判断线段BC与BD的数量关系,直接写出结论;
②请探究线段AC,AD和BE之间的数量关系,写出结论并证明;
(2)如图2,当点C在射线AN的反向延长线上时,BC交射线AM于点F,若AB=4,AC=![]() ,请直接写出线段AD和DF的长.
,请直接写出线段AD和DF的长.
参考答案:
【答案】(1)①BC=BD;②AD+AC=![]() BE;(2)AD=5
BE;(2)AD=5![]() , DF=
, DF=![]() .
.
【解析】试题分析:(1)①结论:BC=BD.只要证明△BGD≌△BHC即可.②结论:AD+AC=![]() BE.只要证明AD+AC=2AG=2EG,再证明EB=
BE.只要证明AD+AC=2AG=2EG,再证明EB=![]() BE即可解决问题;
BE即可解决问题;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K.由(1)可知,△ABG≌△ABH,△BGD≌△BHC,易知BH,AH,BC,CH, AD的长,由sin∠ACH=![]() ,推出AK的长,设FG=y,则AF=
,推出AK的长,设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,由△AFK∽△BFG,可得
,由△AFK∽△BFG,可得![]() ,可得关于y的方程,求出y即可解决问题.
,可得关于y的方程,求出y即可解决问题.
试题解析:(1)①结论:BC=BD,
理由:如图1中,作BG⊥AM于G,BH⊥AN于H,
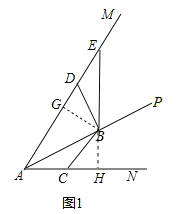
∵∠MAN=60°,PA平分∠MAN,BG⊥AM于G,BH⊥AN于H,∴BG=BH,∠GBH=∠CBD=120°,∴∠CBH=∠GBD,∵∠BGD=∠BHC=90°,∴△BGD≌△BHC,∴BD=BC;
②结论:AD+AC=![]() BE,
BE,
∵∠ABE=120°,∠BAE=30°,∴∠BEA=∠BAE=30°,∴BA=BE,∵BG⊥AE,∴AG=GE,EG=BEcos30°=![]() BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=
BE,∵△BGD≌△BHC,∴DG=CH,∵AB=AB,BG=BH,∴Rt△ABG≌Rt△ABH,∴AG=AH,∴AD+AC=AG+DG+AH﹣CH=2AG=![]() BE,∴AD+AC=
BE,∴AD+AC=![]() BE;
BE;
(2)如图2中,作BG⊥AM于G,BH⊥AN于H,AK⊥CF于K,
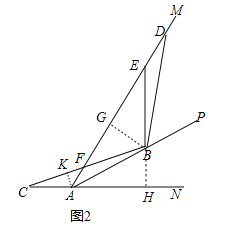
由(1)可知,△ABG≌△ABH,△BGD≌△BHC,
易知BH=GB=2,AH=AG=EG=![]() ,BC=BD=
,BC=BD=![]() =
=![]() ,CH=DG=
,CH=DG=![]() ,
,
∴AD=![]() ,∵sin∠ACH=
,∵sin∠ACH=![]() ,∴
,∴![]() ,∴AK=
,∴AK=![]() ,
,
设FG=y,则AF=![]() ﹣y,BF=
﹣y,BF=![]() ,
,
∵∠AFK=∠BFG,∠AKF=∠BGF=90°,
∴△AFK∽△BFG,∴![]() ,∴
,∴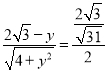 ,解得y=
,解得y=![]() 或
或![]() (舍弃),
(舍弃),
∴DF=GF+DG=![]() ,即DF=
,即DF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解
∵
 <
< <
< ,即2<
,即2< <3.
<3.∴
 的整数部分为2,小数部分为
的整数部分为2,小数部分为 ﹣2,
﹣2,∴1<
 ﹣1<2
﹣1<2∴
 ﹣1的整数部分为1.
﹣1的整数部分为1.∴
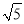 ﹣1的小数部分为
﹣1的小数部分为 ﹣2
﹣2解决问题:已知:a是
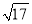 ﹣3的整数部分,b是
﹣3的整数部分,b是 ﹣3的小数部分,
﹣3的小数部分,求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、B两个村庄的坐标分别是(2,1)和(6,3),一辆汽车从原点O出发,沿x轴向右行驶.
(1)当汽车行驶到点M(___________)时离A村最近;
(2)当汽车行驶到点N(____________)时离B村最近;
(3)当汽车行驶到点P(___________)时离A、B两村一样近.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在数轴上表示的数是-2,点B到原点的距离等于3,则A、B两点间的距离是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】台风“杜鹃”给浙江省造成的经济损失达16.9亿元,近似数16.9亿精确到______位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%.
(1)这种商品A的进价为多少元?
(2)现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(
 )
)初中部
a
85
b

高中部
85
c
100
160
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差
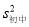 ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.
相关试题

