【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?(直接写出答案,不需要说明理由.)

参考答案:
【答案】(1)证明见解析;(2)当OA=BC时,平行四边形DEFG是菱形.
【解析】
试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=![]() BC,GF∥BC且GF=
BC,GF∥BC且GF=![]() BC,从而得到DE∥GF,DE=GF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
BC,从而得到DE∥GF,DE=GF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)根据邻边相等的平行四边形是菱形解答.
试题解析:(1)∵D、E分别是AB、AC边的中点,
∴DE∥BC,且DE=![]() BC,
BC,
同理,GF∥BC,且GF=![]() BC,
BC,
∴DE∥GF且DE=GF,
∴四边形DEFG是平行四边形;
(2)当OA=BC时,平行四边形DEFG是菱形.
-
科目: 来源: 题型:
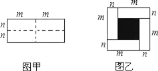
查看答案和解析>>【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)图乙中阴影部分正方形的边长为 (用含字母m,n的整式表示).
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;
方法二: .
(3)观察图乙,并结合(2)中的结论,你能写出下列三个整式:(m+n)2,(m﹣n)2,mn之间的等量关系吗?
(4)根据(3)题中的等量关系,解决如下问题:若a+b=9,ab=5,求(a﹣b)2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
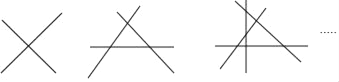
查看答案和解析>>【题目】观察下列图形,第一个图2条直线相交最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交最多有6个交点,…,像这样,则20条直线相交最多交点的个数是( )
A. 171 B. 190 C. 210 D. 380
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )

A.110°
B.80°
C.40°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
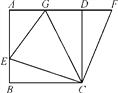
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,则下列叙述不正确的是( )

A. 点O不在直线AC上
B. 射线AB与射线BC是指同一条射线
C. 图中共有5条线段
D. 直线AB与直线CA是指同一条直线
相关试题

