【题目】如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E .
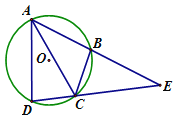
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
参考答案:
【答案】(1) ∠CBE=86°;(2)证明见解析.
【解析】试题分析:(1)根据圆内接四边形的性质计算即可;(2)证明△ADC≌△EBC即可.
试题解析:(1) ∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°.
又∵ ∠ADC= 86°,
∴ ∠ABC= 94°,
∴ ∠CBE=180° - 94°=86°.
(2)∵ AC=EC,
∴ ∠E=∠CAE ,
∵ AC平分∠BAD,
∴ ∠DAC=∠CAB ,
∴ ∠DAC= ∠E.
∵ 四边形ABCD内接于⊙O,
∴ ∠ADC+ ∠ABC= 180°,
又∵∠CBE+∠ABC = 180°, ,
∴ ∠ADC= ∠CBE,
∴ △ADC ≌ △EBC ,
∴ AD=BE .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(3,3 )是正比例函数
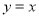 上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.
上一点,点M(m ,0)与点N(0 ,n)分别在x轴与y轴上,且∠MAN=90°.(1)如图1,当N点与原点O重合,求M点的坐标;
(2)如图2,已知m,n都为正数,连接MN,若MN=
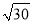 ,求△MON的面积.
,求△MON的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
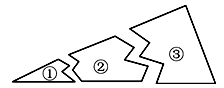
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
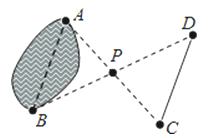
12【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b,当x=2时y的值是﹣1,当x=﹣1时y的值是5.
(1)求此一次函数的解析式;
(2)若点P(m,n)是此函数图象上的一点,﹣3≤m≤2,求n的最大值.
-
科目: 来源: 题型:
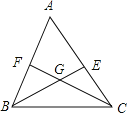
查看答案和解析>>【题目】如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=115°,则∠A= .
【答案】50°
【解析】
试题分析:根据三角形内角和定理求出∠GBC+∠GCB,根据角平分线的定义求出∠ABC+∠ACB,根据三角形内角和定理计算即可.
解:∵∠BGC=115°,
∴∠GBC+∠GCB=180°﹣115°=65°,
∵BE,CF是△ABC的∠ABC和∠ACB的平分线,
∴∠GBC=
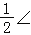 ABC,∠GCB=
ABC,∠GCB=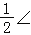 ACB,
ACB,∴∠ABC+∠ACB=130°,
∴∠A=180°﹣130°=50°,
故答案为:50°.
【题型】填空题
【结束】
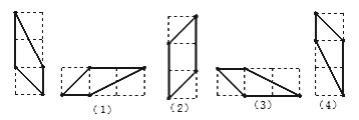
14【题目】如图所示,有(1)~(4)4个条形方格图,图中由实线围成的图形与前图全等的有
________(只要填序号即可).
-
科目: 来源: 题型:
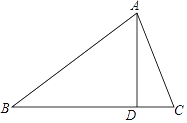
查看答案和解析>>【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
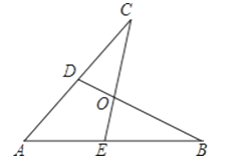
16【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(x﹣2)(x﹣3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是( ).
A. 当m=0时,x1=2,x2=3
B. m>﹣
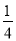
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x﹣x1)(x﹣x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
相关试题

